Today’s guest tutorial comes to you courtesy of X.
Similarity (F)
Recall some of the properties of cosine, as we saw in part 2.
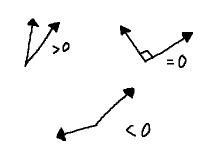
When the angle is small, the cosine's value is close to one. Near right angles, the value approaches zero. With more or less semicircular arcs, the value comes to about negative one. Any other angle falls somewhere in between. On account of cosine's symmetry, this holds both for negative and positive angles.
For this reason, the cosine, and by extension the dot product, offer a sort of similarity measurement between vectors. When two unit vectors are nearly aligned, their dot product is close to one. They are approximately the same. On the other hand, vectors perpendicular to one another have, in some sense, nothing in common, answering to values near zero. Negative products, finally, correspond to vectors facing in more or less opposite directions, completely so for negative one—they are related, but in a "everything my neighbor does, do the opposite" fashion.
(NOTES: Component for non-unit vectors)
This is a key component of many lighting models, for instance. Every point on an object's surface has a unit vector, the normal, perpendicular to it. In addition, each point looks toward the light source (rather, the light arrives from it, but we use the reverse of this direction). At each point we see compare the normal and "look at" direction. The more directly light hits, the more alike these are, and consequently the brighter that spot. The object gets steadily darker as the similarity tapers toward zero, negative values being rejected outright. For examples in Corona, see the directional or point light-based normal map effects. (TODO: image)
It was hinted earlier that we are only dealing with a fairly specific sort of vector, namely those belonging to plane geometry. Similarity hints at other uses we might explore, as well as how cosine might be applied outside a strictly geometric context. Identifying properties like similarity and teasing out their useful implications is also key to generalizing geometric operations, the dot product among them.
(IMAGE: 12)
The determinant (G)
A shortcoming of the dot product, by way of the underlying symmetry, is that we cannot say which side one vector lies on relative to the other. The vector $ \mathbf{v} $ and its reflection seen in the last section, for example, are equally similar to $ \mathbf{w} $, despite their obvious differences.
Similarity does give us a way to approach this, however. Asking "Which side is this vector on?" is much like wondering "How is it similar to a perpendicular vector?". We know of two candidates here: the perp operator and the rejection. The rejection is worthless in this situation, since it always points toward the vector—yes, the rejection gets rejected—but the perp operator gives us exactly what we need, owing to its reliable orientation.
The question thus boils down to "How similar is this vector to the result of the perp operator?". $ \dotvw{v}{w^{\perp}} $ yields one sign on one side of $ \mathbf{w} $, the reverse on the other, or zero should the vectors align. (Which sign is which, of course, is subject to our choice of perp operator.)
(NOTES: join)
Both the projection and the result of the perp operator are perpendicular to $ \mathbf{w} $. Either they have the same or opposite directions; they are perfectly similar or dissimilar, pending normalization. If we call the angle between them $\phi$, we can say $ \cos\phi = \pm 1. $
Consider their dot product: $ \dotvwparen{w^{\perp}}{v - proj_w v} $.
As pointed out earlier, dot products distribute over subtraction, so this may be rewritten as $ \dotvw{w^{\perp}}{v} - \dotvw{w^{\perp}}{proj_w v} $. Also mentioned was that $ \mathbf{proj_w v} $ has the same direction as $w$—basically, $v$ gets flattened onto it. As such, it will $ \mathbf{w^{\perp}} $ is perpendicular to it as well. This makes their dot product zero, of course, leaving us with $ \dotvw{w^{\perp}}{v} $. Interestingly, this is precisely our "above or below?" similarity condition.
So long as we stay consistent, the choice of perp operator is fairly arbitrary. Selecting one and working out the components, then: $ \softerdotvw{\vcomps{w_y}{-w_x}}{v} $, or $ v_x w_y - v_y w_x $.
This is the determinant. As noted, this is equal to the earlier similarity, whose sign tells us what side $ \mathbf{v} $ lies on with respect to $ \mathbf{w} $.
(IMAGE: 13)
(NOTES: join)
Now, $ \mathbf{w^{\perp}} $ simply swaps the components $ \mathbf{w} $ and changes one of their signs. All of this comes out in the wash when we take its length, meaning $ \vlen{w^{\perp}} = \vlen{w}. $
From the dot product-cosine connection, we saw that $ \lenvw{v}{w}\cos\theta = \dotvw{v}{w}. $ At this point, we have accounted for everything except one of the vector lengths. So what is $ \vlen{v - proj_w v} $?
Of course, we could just grind it out, although the results will not be terribly enlightening. Instead, review the image of the rejection above, then recall the aforementioned dot product-cosine derivation, in particular where the right triangle's height was found. The rejection is exactly the side in question, so it follows that it has length $ \vlen{v}{\mid\sin\theta\mid} $. Note the absolute value; sine will go negative if the angle does, whereas lengths are positive. (In a right triangle, the non-right angles cannot get very wide, so negative cosines are a non-issue.) (TODO: image?)
Assembling all of this: $ \pm\vlen{w}\vlen{v}{\mid\sin\theta\mid} = v_x w_y - v_y w_x. $
The ± out front renders this somewhat unwieldy. Thankfully, $ \pm{\mid\sin\theta\mid} $ simplifies to $ \sin\theta $; sine has the aforementioned ability to go negative, so all is well. In the end, we have a sort of companion to the dot product-cosine equation: $ v_x w_y - v_y w_x = \lenvw{v}{w}\sin\theta. $
(IMAGE: 14)
(NOTES: join)
Our analysis thus far has considered vectors overlain on the sides of a right triangle. But several times, we came up with this triangle by decomposing a more general triangle. We can work backward from this insight, interpreting the side with sine-based length as an altitude. The other leg was already a projection in in the last few sections; with that in mind we can just call the full base $ \mathbf{w} $.
As we saw in part 1, the area of a triangle is $ wh \over 2 $. In our vector-sided context, this becomes $ {\lenvw{w}{v}\sin\theta} \over 2 $.
This is almost exactly the determinant, of course. It tells us that the determinant is equal to twice the area of the triangle described by two vectors, say $ \mathbf{v} $ and $ \mathbf{w} $. A doubled area is rather awkward, but we can introduce a second triangle to account for it. If we then rotate this clone and affix it to the original, we end up with a parallelogram, an object with two pairs of parallel sides. (TODO: image)
Quite often, the determinant is phrased in these terms instead, as the area of such a parallelogram. For instance, in the case of matrices and linear transformations, this more naturally mirrors the underlying coordinate systems.
(IMAGES: 15, 16)
Point in triangle (H)
Something strange is going on. We want to all that trouble getting the determinant's sign squared away, then it shows up in a formula for area! What does a negative area even mean?
First things first, the absolute value of this area carries the usual, intuitive meaning of the space taken up by the triangle or parallelogram. No surprises here.
The determinant was the same as the "which side?" similarity and also lends its sign to this area. The upshot of this is that the area's sign likewise conveys this side information. This is a bit of an odd pairing: area and side. Where might we put it some use?
In formulating the determinant above, we used the choice of perp operator that says one vector, say $ \mathbf{v} $, is on the positive side of the other, say $ \mathbf{w} $, when oriented counterclockwise to it. This is the so-called right-hand rule: starting with our fingers aligned to one vector, we rotate them to align with the other, all the while keeping our thumb pointing up; a positive angle proceeds from $ \mathbf{w} $ to $ \mathbf{v} $ is described by the right hand, otherwise the left. (TODO: images)
(NOTES: Breaks up the flow? Put the rule part in the perp operator section, maybe.)
(NOTES: Arggh, at any rate, this is proving hard to organize...)
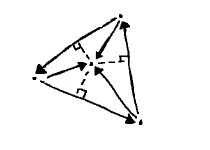
Now, imagine a triangle, with vectors along its sides, oriented so they traverse a loop around its sides. Furthermore, this triangle contains a point. From each side, we can trace another vector toward this point, starting from the tails of these side vectors.
Each of the tail-to-point vectors are obviously above their respective sides, according to our right-handed convention. This will not be so, however, for a point outside the triangle, as seen on the right: on some sides the determinant is positive, on others negative, or zero when the point is on the side. Thus, we can establish containment for a point by checking that all three are positive. (TODO: image)
Together, a side and its tail-to-point vector describe a triangle, nested inside the larger one. For that matter, the implicit third side coincides with the tail-to-point vector of the next side in the sequence, so these constitute the full triangle. It seems only natural that these individual areas should sum to the total amount. (TODO: image)
These same circumstances prevail when the point lies outside the larger triangle, however, so we find ourselves in a bit of a quandary. As the picture shows, the pieces make up a larger object: the sum is not greater than its parts! Must we restrict ourselves to the inside case?
These triangles, being vector-sided, are amenable to the new area formula. These areas can be positive or negative, of course. This accounts for the extra space: whenever one of the triangles is "too positive"—the point is "above" its base, but so much it spills out of the larger triangle—another one makes up for it by having negative area—here, the point is "below" the base. In the end, the signed areas do indeed sum to the (positive) area of the full triangle.
(IMAGES: 18, 19)