Today’s guest tutorial comes to you courtesy of X.
The method of exhaustion
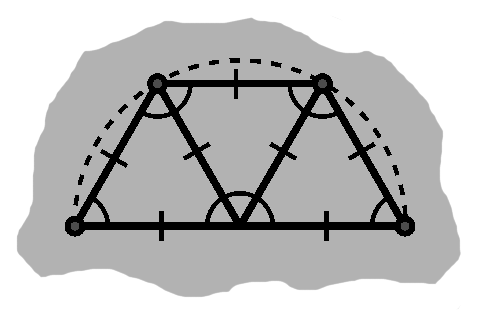
We know, from the triangle postulate, that all angles in an equilateral triangle measure 60°. We may therefore pack three of them together along a line, as depicted in K-2.
Three of the corners coincide. Since all sides in an equilateral triangle have the same length, the remaining corners must be equally far from this point. This lets us interpret the two sides flush with the line as a diameter, with the whole arrangement being on half a circle.
Chords resemble arcs, so summing their lengths should give us a rough approximation of the semicircle's arc length: three times the radius, in this case.
As we saw earlier, an isosceles triangle will divide into congruent right triangles. Equilaterals are a special case of isosceles, so we can do so here: this bisects our central angles, now measuring 30° apiece, and introduces two new corners midway along each chord.
If we hoist these corners onto the semicircle, our right triangles become isosceles themselves. Additionally, we can replace each of our old chords by two new ones that hew even closer to our arcs. An example can be seen in figure K-3.
Once again, we can sum up the chord lengths, six of them now: \begin{align} 6\,\rm{crd}\,30^\circ & = 6\left(2\sin \frac{30^\circ}{2}\right) \\ & = 12\sqrt{\frac{1 - \cos 30^{\circ}}{2}} \\ & \approx 12\sqrt{.06699} \\ & \approx 3.10583 \end{align}
Since we ended up with isosceles triangles, we can repeat the division process, halving our angles and doubling the number of chords in doing so. With twelve chords and 15° central angles, our arc is around $3.13935$ long.
The calculation generalizes for the i-th iteration, with $i = 1$ being the case with equilaterals: \begin{align} \mathrm{\text{arc length}} \approx 3\left(2^i\sin \frac{60^\circ}{2^i}\right) \end{align} On each pass, we leave less space between the chords and arcs. This refinement process will in fact go on indefinitely, but the adjustments quickly become vanishingly small. After just a few steps our values are in the neighborhood of $3.14159.$
This is $\boldsymbol{\pi},$ perhaps the most famous constant in all of mathematics!
In code, the procedure described above might look like
local sqrt = math.sqrt
local function Sin ( steps )
local cosa = sqrt( 3 ) / 2 -- start with cos(60 degrees)
for i = 1, steps - 1 do
cosa = sqrt( (1 + cosa) / 2 ) -- get cos(angle / 2)
end
return sqrt( 1 - cosa^2 ) -- sin(angle)
end
function PI ( n )
local steps = n + 1
local count = 2^steps
return 3 * count * Sin( steps )
end
print( PI( 13 ) ) -- prints 3.1415926453212 on my machine
-- N.B. this numerical precision problems will overwhelm this
-- algorithm if we push `n` much furtherRound and round we go (K)
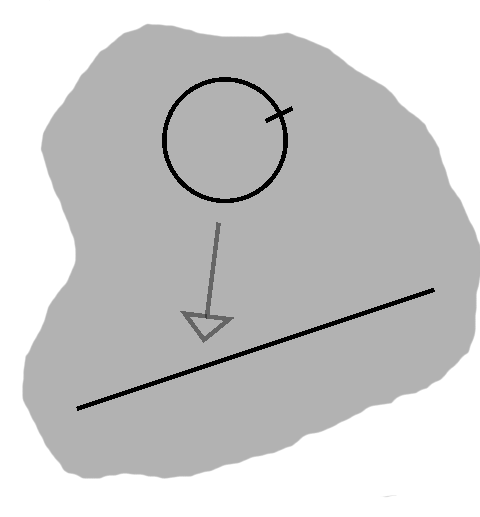
Consider something like thread, wound around a spool.
Now, suppose we have enough thread to wrap around once, so the two ends just meet. No stretching allowed!
Obviously, this thread has a length. As this thought experiment demonstrates, this length applies in some sense to the spool, as well, more specifically its circular cross-section. This distance around a circle is called its circumference.
The thread is easily measured, of course. Once unrolled, its length is just the straight-line distance from one end to the other.
Thread was one example, but we could come up with many more, in all shapes and sizes. Soon enough, a relationship seems to emerge: one revolution of the "thread" always shows a circumference just shy of 6.3 times the radius of the "spool".
Traditionally, rather than relate the circumference to the radius, which reaches only halfway across the circle—that is, from any given point on the boundary to its center—the diameter is preferred instead. Nothing fancy here; the diameter is simply twice the radius. The ratio of the circumference to the diameter, then, comes out to approximately 3.14159...
This is the famous constant, $ \pi! $
As expressed in mathematical symbols, then, circumference is given by $ 2 \pi r. $
Continuing with the wraparound approach, we can wrap "threads" one-fourth, half, and three-quarters of the original length around our circle. It should come as little surprise that these appear to span the same fraction of the circumference. The facts bear this out for arcs in general, giving us arc lengths of $ (2\pi r)t $, with $ 0 \le t \le 1 $ being the ratio of arc to circumference.
Working with $t$ is a bit awkward, since we then basically already know our arc length. We can streamline this by using angles between 0 and $2\pi$ to traverse the circle. Then arc length is simply $ L = r\theta. $ In the unit circle, for that matter, angle and arc length are one and the same.
Such angles are known as radians. Frequently, in geometry, and almost exclusively in trigonometry, these will be the preferred unit of angular measure. Rather than 90°, 180°, 270°, and 360°, it is quite common to see $ {\pi\over 2}, $ $\pi,$ $ {3\pi\over 2}, $ and $ 2\pi $ in mathematical texts.
Thankfully, the ranges $ [0, 2\pi] $ and $ [0, 360] $ differ only by a constant scale factor. A measurement denominated in degrees can be multiplied by $ \pi \over 180 $ to convert it to radians, while $ 180 \over \pi $ will achieve the reverse. In fact, Lua—and thus Corona—even provides a couple helper functions, so we need not even remember these values: math.deg and math.rad.
local rad = math.rad
local sin = math.sin
function PI2 ( n )
-- At the outset, we have three 60-degree triangles, or 3 * (2 * sin(30 degrees)). At each
-- iteration, we halve all the angles and double the triangle count.
local count = 2^(n + 1)
return 3 * count * sin( rad( 60 / count ) )
end
print( PI2( 15 ) ) -- prints 3.1415926534561...
print( math.pi ) -- ...and 3.1415926535898Wheels within wheels (L)
For completeness, we can also look at the area of a circle.
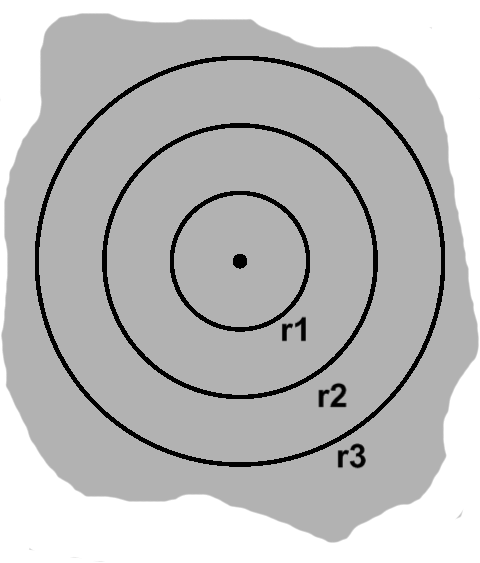
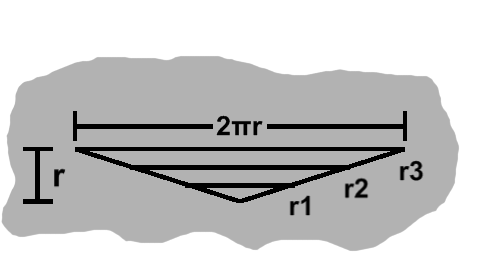
Within a circle, we can highlight any number of concentric circles, which is to say smaller ones that share the same center. In the image on the left, for instance, circles of radius $r_1$ and $r_2$ are nested inside a larger circle of radius $r_3$.
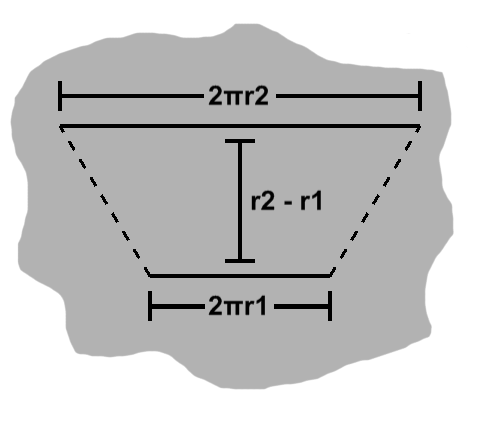
When we consider two consecutive circles, we see that they form a ring. As mentioned, every point on a given circle is equally far from its center, so if we draw a line through two concentric circles, the thickness of this ring will be given by subtracting the lesser radius from the greater one, e.g. $ r_2 - r_1 $.
Now, earlier we saw the connection between circumference and straight line distance. With that in mind, we can draw some conclusions about our pair of circles.
The thickness $ r_2 - r_1 $ was the distance between the two circles, so it makes sense as a height. However, $r_2$ is wider than $r_1$, so we have something that is not quite a rectangle.
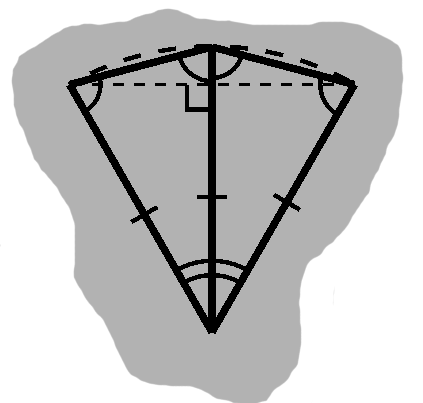
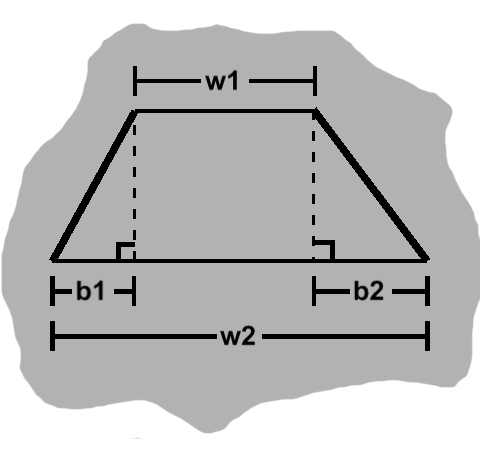
This is what is known as a trapezoid, a geometrical object with two parallel sides, usually of different lengths, and a common height.
As seen in the image, a trapezoid comprises a rectangle and two right triangles. The longer base has length $ w_2 = w_1 + b_1 + b_2, $ the rectangle has area $ w_1 h $, and the triangles have areas $ b_1 h \over 2 $ and $ b_2 h \over 2 $.
Together, the triangles have area $ (b_1 + b_2)h \over 2 $. We can replace the sum of the triangle bases, using what we know from the length of the longer trapezoid base: $ (w_2 - w_1)h \over 2 $.
Adding the rectangle area to this, our trapezoid has a total area of $ w_1 h + {(w_2 - w_1)h \over 2} $.
Simplifying a little further: $ (w_1 + w_2)h \over 2 $.
Worth noting is that, if the shorter length is zero, this becomes the triangle area formula. (If both sides are equal, on the other hand, we have a rectangle.)
This may be applied to our unrolled rings. The two sides are their respective circumferences, with the thickness as the height. This is $ (2\pi r_1 + 2\pi r_2)(r_2 - r_1) \over 2 $.
This reduces to $ \pi(r_1 + r_2)(r_2 - r_1) $ and in turn $ \pi(r_2^2 - r_1^2) $.
The point about lengths of zero is worth revisiting quickly. Since the side lengths are circumferences in this model, for one to be zero would mean a radius of zero. For consistency, we can call this radius $r_0$. This might seem a little strange, yet it fits snugly into the definition of a circle: all points a distance of zero from the center, the only such candidate being the center itself!
The upshot of this last bit is that the innermost circle can also be streamlined into the ring formulation.
Now, something interesting happens when we start adding these trapezoids together. Here are our three areas lined up: \begin{align} area_1 & = \pi(r_1^2 - r_0^2) \\ area_2 & = \pi(r_2^2 - r_1^2) \\ area_3 & = \pi(r_3^2 - r_2^2) \end{align} Comparing subsequent lines, we see $ r_1^2 $, followed by $ -r_1^2 $, and likewise for $r_2$. Thus, after summing all these areas together, what remains is $ \pi r_3^2 $. Since $r_3$ was the outermost radius, we can write the more familiar area formula, $ \pi r^2 $.
Since all these intermediate terms cancel, we could have found the area with more and more circles, even pushing it to the limit where the distance between consecutive circles is infinitesimally small. This might ring a bell to those acquainted with calculus—indeed, the circle area turns out to be the integral of the circumference.
(NOTES: sectors)
(NOTES: Trapezoids slightly more general, e.g. triangle on each side)
The area formula offers us another insight. $ \pi r^2 $ is exactly the area of a triangle with base $ 2\pi r $ and height $r$. And indeed, if we stack all our trapezoids (including the "trapezoid" with one side 0), they coalesce into that very triangle!