Today’s guest tutorial comes to you courtesy of X.
Discussing each side's terms
Triangles are a fitting place to begin.
As the name suggests, these are objects with three angles.
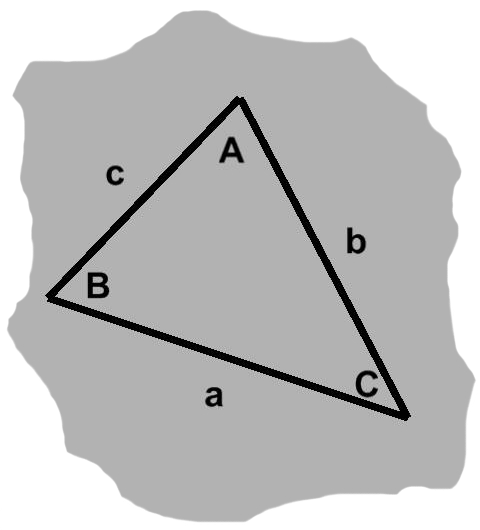
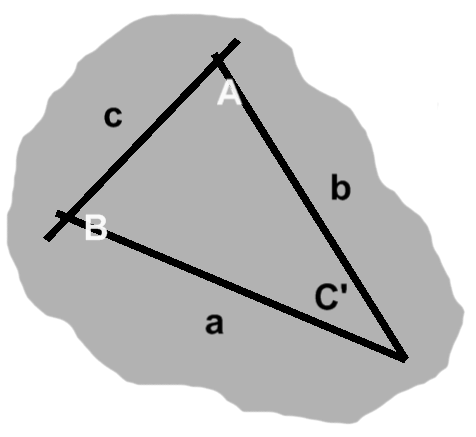
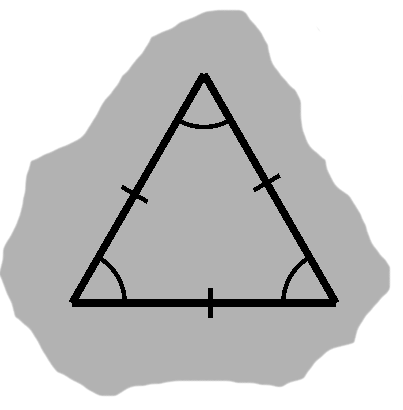
Yet this only tells us part of the story. It is equally true that a triangle is a three-sided object. A proper treatment must take both views into account. The triangle in figure A-1, for instance, has angles $A,$ $B,$ and $C,$ as well as sides $a,$ $b,$ and $c.$
There are some noteworthy relationships between angles and sides.
To begin, we might speak of a side being "across from" some angle. This relationship can be seen in figure A-1: each uppercase letter labels an angle, whereas its lowercase counterpart designates the side opposite that angle. Side $a$, for example, is opposite angle $A.$
The remaining two sides, those "next to" the angle in question, are adjacent. The angle itself is included between these sides. Continuing with our example, these would be sides $b$ and $c.$
The rather general triangle in figure A-1 might seem difficult to approach, but notice what happens if we tilt our heads to the right just a bit: side $a$ appears to be horizontal, though none of the angles have changed and all sides remain just as long.
From this perspective, certain obstacles simply go away. We suddenly have a notion of "up", for instance, suggesting avenues we might explore. This demonstrates a technique common in mathematics: we transform one thing into something simpler, perform some action on that, then reverse-transform the results.
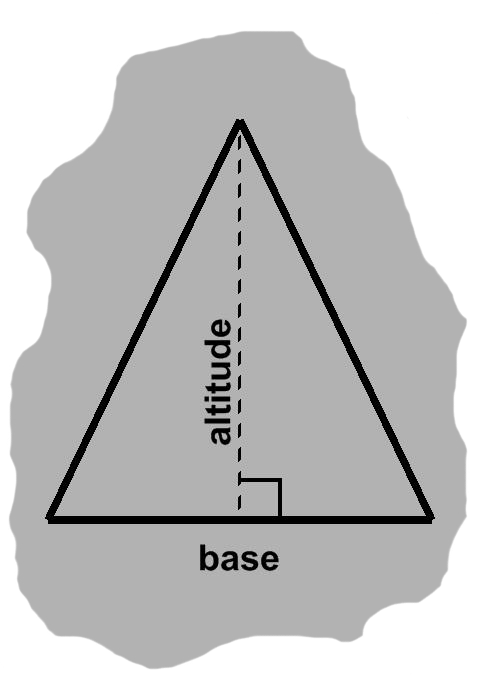
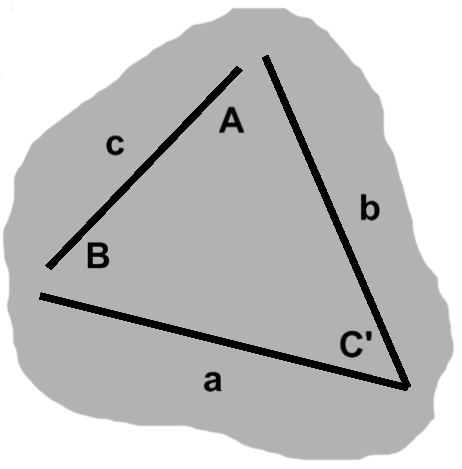
Throughout this article, for instance, we will often use "nice" triangles, such as the one in figure A-2, but these can be understood as the middle step between two rotations that happen offscreen: align one side → do our analysis → restore original orientation.
Given a horizontal side, we may draw a line segment straight up from it toward the corner which it lies opposite, the dashed vertical segments in figures A-2 and A-4 being examples. Such a segment is known as an altitude. Its length is called a height and the triangle side is a base.
Any side will do as a base, though in many problems one will stand out, for one reason or another. Each choice is paired up with a different altitude, of course.
An altitude is said to be perpendicular to its base: we have the junction of a horizontal segment with a vertical one, resulting in a right angle. Conventionally, such angles are depicted by squares. The altitude and base will often make a T when they meet, perhaps an upside-down one as in figure A-2. Naturally enough, the ⊥ symbol has come to indicate perpendicularity.
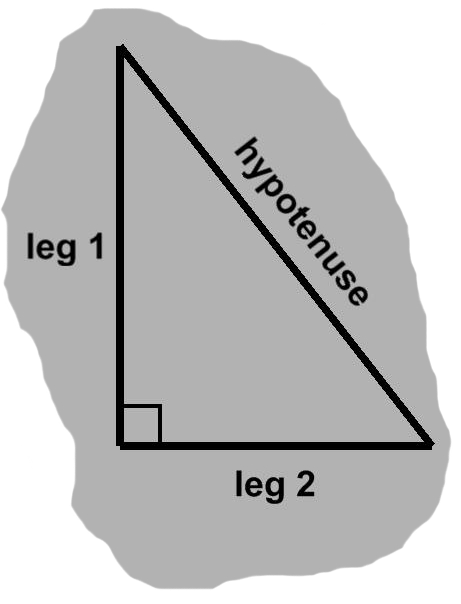
If the altitude and one of the sides overlap, we have a right triangle, as in A-3. In such a triangle, the side opposite the right angle is known as the hypotenuse. The adjacent sides are called legs.
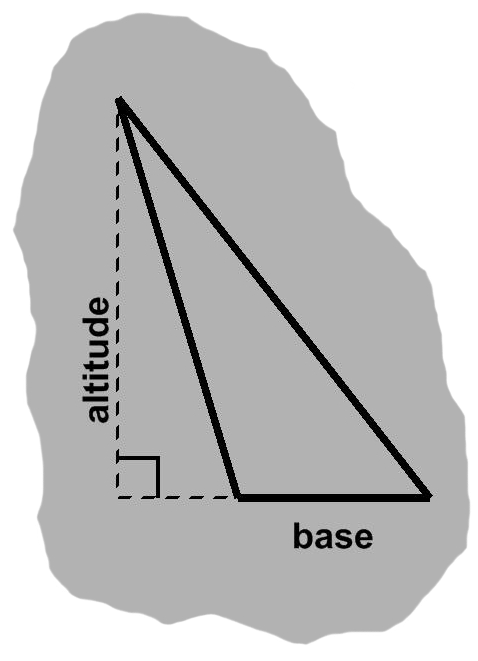
Angles wider than a right angle are said to be obtuse. (Their narrower cousins are acute.) When a base is adjacent to such an angle, both remaining sides lean either left or right, so that their corner is no longer above the base. As a result, the altitude will be outside the triangle. The base and altitude will not even meet, unless the former is extended artificially, as in A-4.
Considering different angles
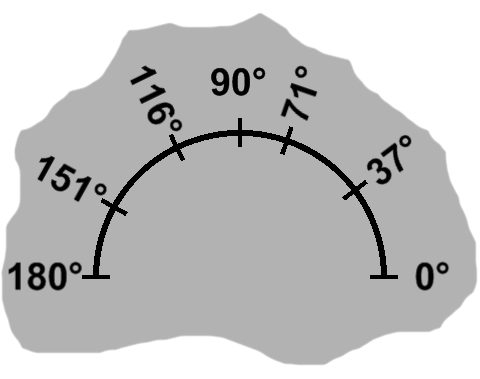
In real-world situations, we will nearly always want something more precise than "wider (or narrower) than a right angle". With this in mind, angles are assigned a measure that increases in proportion to the separation between sides.
Measurements are denominated in degrees in this article, though other units are available as well. In a triangle, the range of angles begins just after 0° (sides together, thus no angle), runs through 90° (right angles), and ends a bit shy of 180° (sides fully apart, in a straight line).
Many sources label corners rather than angles, adopting a different scheme for the latter. If a triangle had corners $A,$ $B,$ and $C,$ it would be typical under these circumstances to see angles such as $ \angle ABC. $ This particular choice would refer to the angle at corner $B$ or, more specifically, included between the segment from $A$ to $B$ and the segment from $B$ to $C.$ The measure to go along with it would be written as $ \measuredangle ABC. $ For simplicity, this article will continue to label angles directly. Additionally, we will use this notation interchangeably for both angles and their measures, according to context.
By interspersing one or more lines, an angle can be divided up into two or more adjacent angles. B-2 shows such a situation. Conversely, neighboring angles may be coalesced. We can measure the full angle simply by adding up the lesser ones.
Adjacent angles share a side and corner. Thus, a given angle may be adjacent to one or two other angles, or none at all.
Garden-variety angles are often denoted by one or more arcs, as in figures B-2, B-3, and B-4. When two or more angles are shown with the same number of arcs, these angles are understood to have equal measurements. Varying numbers are typically a cue that the angles need not be equal (but could be). They might instead mean the angles must in fact be different, but usually this stronger condition will be spelled out.
(NOTES: Can use double angles, and thus half ones, to show linearity of angle)
(NOTES: Further below can show overlap of angle... corner and part of side)
Sticking together
A little thought experiment is now in order.
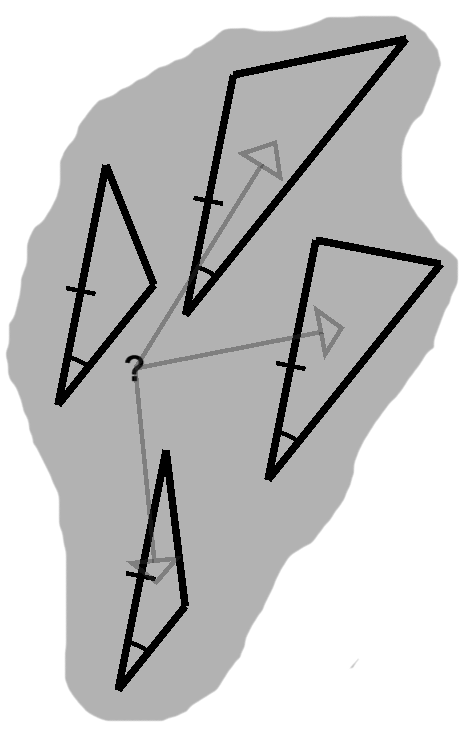
Consider what would happen if, beginning with the triangle from figure A-1, we were to narrow or widen one of its angles, say $C.$ On top of this, suppose no other angle or side length was allowed to change.
Figures C-1 and C-2 depict a couple possible outcomes, following only slight variations in $C.$
A narrower angle results in the situation shown in figure C-1, where the adjacent sides, $a$ and $b$, arrive at the opposite side "early" and penetrate it—rather than meet up with its endpoints and form corners—then press on just a bit farther.
With a wider angle, on the other hand, the sides stop short of $c$, if only barely, but also veer away from it. Figure C-2 is an example of what we might see.
In order to repair one of these objects, restoring its triangularity, we would need to slide side $c$ either forward or backward, until it was in line with the endpoints of both $a$ and $b$, then either shrink or extend it for a snug fit. Barring that, neither case deserves to be called a triangle.
Small adjustments to a side length would produce similar breakage, assuming the remaining properties were held fixed.
As our short investigation shows, triangles possess a very rigid structure. Angle measures and side lengths are closely related, with only a bit of give-and-take being possible. Consequently, once a few of its angles and sides have been pinned down, so are the others. This works in our favor: knowing only some of a triangle's properties, we can deduce the rest!
When dealing with multiple triangles, this is especially important. Angles and sides will accumulate quickly; the more of them we can ignore, the better off we are.
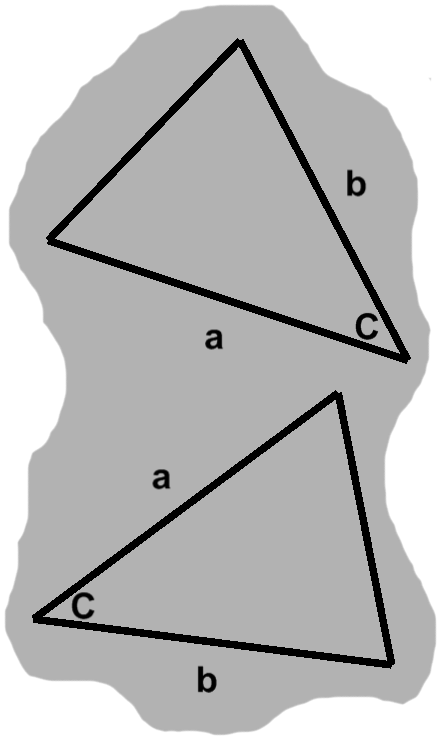
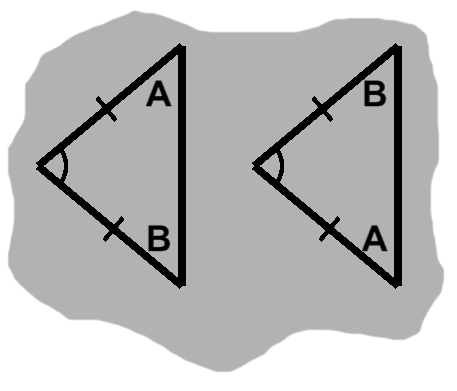
Suppose we have two triangles, $T_1$ and $T_2,$ on hand. Taking $T_1,$ we measure one of its angles plus the adjacent sides, labeling them as $C,$ $a,$ and $b$ respectively.
Say we then shifted our attention to $T_2.$ When measured, one of its angles turns out to be exactly as wide as $C.$ These things do happen, of course, so it goes unremarked.
As we measure the angle's adjacent sides, further similarities emerge: one has the same length as $a,$ the other is as long as $b.$ $T_1$ and $T_2$ have a common side-angle-side sequence. If matching parts were assigned the same labels, we have something like figure C-3.
When we only knew an angle and one of its adjacent sides, $T_2$ was still quite malleable. One of its angles was still totally independent at this point. This scenario is depicted in figure C-4: the triangle may not assume any shape, since part of its structure is indeed locked down, but limitless possibilities exist nonetheless. (Slash marks serve the same purpose for sides that arcs do for angles, with matching counts indicating equal lengths.)
Introducing the second adjacent side will bring us back to our earlier predicament, where any change would upset a delicate balance. This has an extremely important converse: a common side-angle-side sequence means that two triangles are the same.
(NOTES: Is the first half of this clear? Realized it could be more intuitively demonstrated by overlap...)
EXERCISES
1. What other theorems can we use to compare triangles, based on angles and sides?
2. Do these theorems have the same guarantees as side-angle-side?
Identical twins
Properly speaking, the two triangles are congruent. This has a few (equivalent) definitions.
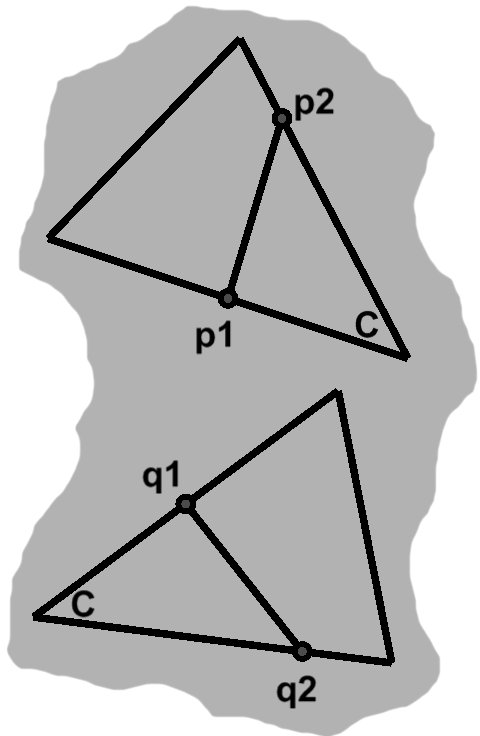
Suppose we have a triangle and decide to traverse its boundary. Each step of the way, we compare our current location to every other one on the same triangle, finding the distance between them. (We will soon see how to perform such calculations.)
At the same time, we examine corresponding points on a congruent triangle. In every instance, the results will be identical.
Figure D-1 is a snapshot of this process. On one triangle, we have chosen two points, $p_1$ and $p_2$, in the middle of one side and three-quarters of the way along another, respectively. On a second triangle, $q_1$ and $q_2$ are equally situated. (Corresponding sides have the same lengths, of course.) Whatever distance lies between $p_1$ and $p_2$ also separates $q_1$ from $q_2$.
When all lengths match, we have congruence. Comparing infinitely many pairs of points is impractical, to say the least, but captures what is going on numerically.
Alternatively, we may speak in terms of rigid motions. These are geometric operations that preserve an object's size and shape: changing its position, rotating it, or taking its mirror image. If we start with one triangle and are able through some combination of these motions to make it perfectly overlap another, the two triangles are congruent. In figure C-3, as an example, we can rotate one of the triangles and move it atop its companion.
The two approaches are not at odds. Overlap is the visual manifestation of all lengths being in agreement, and vice versa.
(NOTES: Either move this before the last section (with appropriate edits) or use overlap to show side-angle-side in effect)
A look in the mirror
An isosceles triangle, where two sides have the same length, shares a side-angle-side sequence with one of its own mirror images. It will therefore be congruent to this "other" triangle.
On account of common lengths, the triangle and mirror image already coincide. With some separation, they might look something like figure E-1. For the initial overlap to have been possible, angles $A$ and $B$ must be equal.
In an equilateral triangle, all sides have the same length.
By restricting ourselves to a couple sides, we can approach this as an isosceles triangle. This will tell us that two angles are equal. Choosing another pair of sides, we can repeat the process, giving us another match. Only three angles are possible, so one of them must show up twice.
For instance, say angles $A$ and $B$ are equal in the first case, $B$ and $C$ in the second. Since they have $B$ in common, $A$ and $C$ ought to match as well. The third pair of sides will confirm this.
TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE
In the less specific isosceles case, we can cut the third side in half, as in E-3. In doing so, we get two triangles with a side-angle-side relationship.
Because this creates two new angles, these must be equal to one another. Since they came from what was originally a line, they must be supplementary, and thus right angles.
The new common side splits the remaining angle, as well. Since these new angles must be equal, each must measure half the original.
We call such sides perpendicular bisectors.
TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE