Today’s guest tutorial comes to you courtesy of X.
Constructing a rectangle
We ended the last article with a brief foray into isosceles triangles, where we saw that these would decompose into two congruent right triangles.
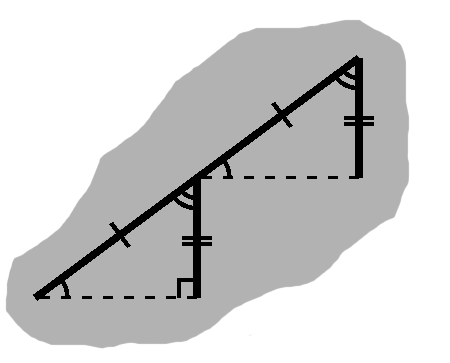
We can do some transformations so that these two parts line up, as in Figure A-1.
Since the two triangles are in the same orientation with one of the corresponding sides lined up, these coalesce into a single segment. Additionally, we know the side with two ticks is perpendicular to the dashed side, in this case to both of them.
We have three angles meeting, where the triangles come together: the angle with one arc, a right angle, and the angle with two arcs.
Together these form a line, so their measures sum to 180°. Half of this comes from the right angle. The one- and two-arced angles—$A$ and $B$ for short—must therefore be complementary: $\measuredangle A + \measuredangle B = 90^\circ.$
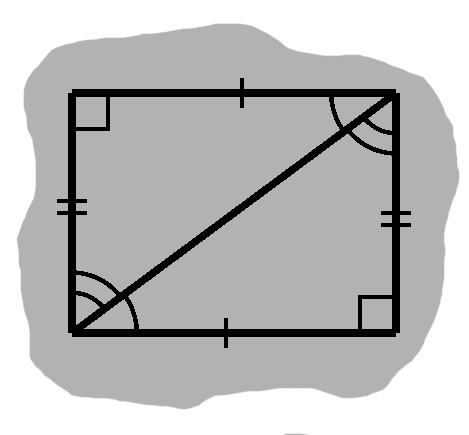
We can arrange our triangles in a different way, so that they combine into a four-angled and -sided object, as in A-2.
Two right angles carry over intact from the triangles. In the other corners, we have pairs of adjacent angles. But we know these are complementary, so they become right angles as well.
Lastly, as the markings show, opposite sides have the same length. Our object is a rectangle.
Thus, a rectangle is simply two congruent right triangles packed together.
(NOTES:Isosceles not actually necessary building block, could simply label angles A and B outright)
Triangles in space!
Given a rectangle, we might try packing it full of smaller objects.
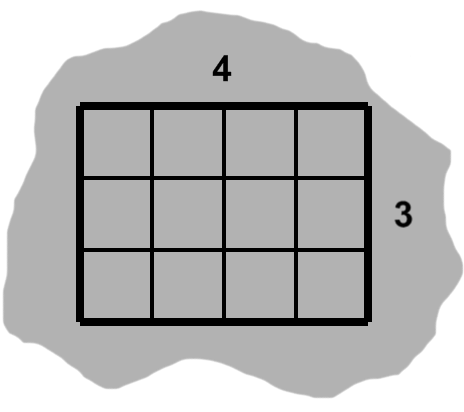
In figure H-1, we have a rectangle four units wide by three units tall. (Our unit in this case is generic, but in practice could be feet, meters, any of their derivatives, and so on.) It contains several one-by-one rectangles, or unit squares.
These squares form a grid, so we can easily count them. Each row consists of the same number of squares, so we need only multiply our column and row counts together. The rectangle in our example is able to fit twelve unit squares.
We might instead say that it has an area of twelve square units, or 12 units².
Our counting strategy holds in general. A rectangle's area is given by its width times its height, often written $ wh. $
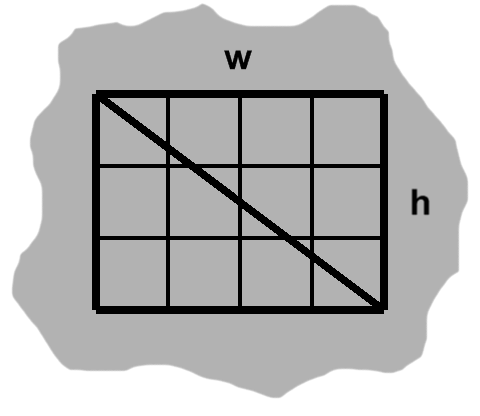
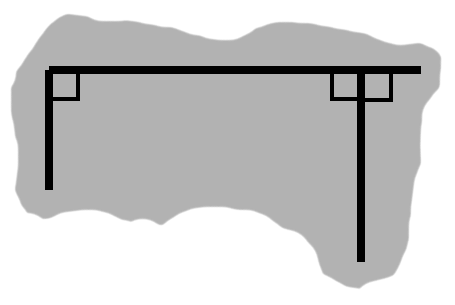
Now, if we slice a rectangle diagonally, from one corner to another, we end up with two triangles, as in figure H-2.
A rectangle, by definition, has four right angles. If two sides both happen to be perpendicular to a third side, they will be parallel to one another.
Figure H-3 demonstrates why this is so. By supplementing one of the angles, we obtain another right angle. We then have corresponding angles, which arise in the presence of parallel lines. Since this transpires in all four cases, we can deduce that the rectangle has two pairs of parallel sides: left and right, bottom and top.
Since distances remain fixed between parallel segments, it follows that a rectangle's parallel sides have equal lengths. In figure H-2, the left side is between the bottom and top sides, so it also has length $h,$ like the right side. The same holds true for the bottom and top sides with $w.$
By side-angle-side, our divided rectangle has become congruent triangles. As we know, these can be moved and rotated to overlap. Each triangle therefore occupies the same amount of space.
Area and space basically express the same idea. Each triangle has half the area of the original rectangle. An area formula for right triangles immediately follows: $ {wh \over 2}. $
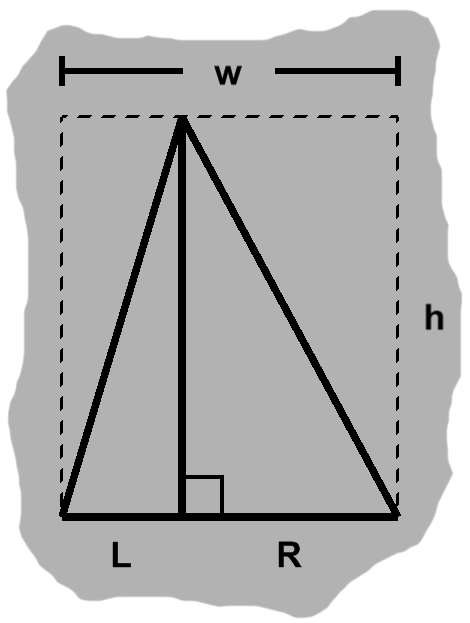
Earlier, in figure A-2, we saw that an altitude decomposes a triangle into two right triangles with shorter bases. A base $w$ units wide divides into sub-bases with widths $L$ and $R,$ as in figure H-4.
From our new formula, the areas of these child triangles are $ Lh \over 2 $ and $ {Rh \over 2}. $ Adding them together gives us a total area of $ {(L + R)h \over 2}. $ Of course, $ L + R = w, $ so the area of the original triangle is in fact $ {wh \over 2}. $
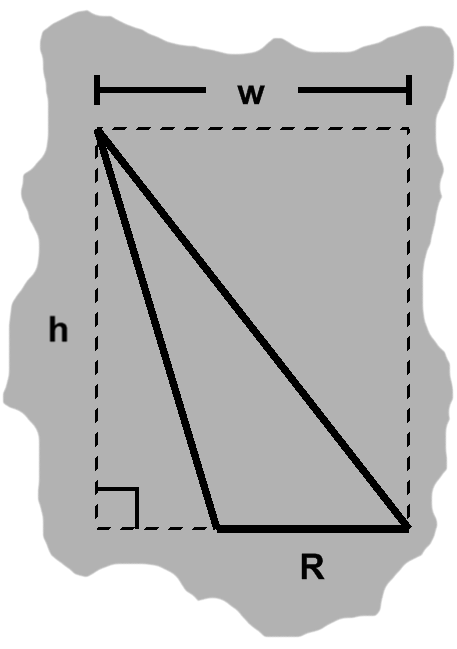
When dealing with an obtuse angle, our approach is slightly different. Assuming $w$ is still the width of the enclosing rectangle, our triangle's base will be a shorter length, $R,$ as in figure H-5.
As we saw earlier in figure A-4, the base in these cases can be extended to intercept the altitude. The augmented triangle this produces is a right triangle, with area $ {wh \over 2}. $ Furthermore, the added-on part is one as well, measuring $ { (w - R)h \over 2 } $.
The area of our original triangle will be the augmented area minus that of the extension: $ {Rh \over 2}. $ Despite a slight change of circumstances, $R$ is also the width of the base, just as $w$ was in the previous two cases.
In general, triangle area is given by $ {bh \over 2}, $ where $b$ is a base width and $h$ the corresponding height.
As an aside, with our four-by-three rectangle, we end up with two triangles of area 6 units². While this still happens to be an integer, the original packing of whole unit squares no longer corresponds to the shape: the area is now dispersed across the squares, with many of them only partially full, as a quick look at figure H-2 will tell us. This ought to provide some insight into how the notion of area generalizes.
EXERCISES
1. Use smaller squares to represent a triangular half rectangle, making sure these almost add up to the proper area. Doing this, can we ever get a perfect fit?