Today’s guest tutorial comes to you courtesy of X.
Linear interpolation
Returning to an earlier point, we mentioned that a similar triangle entailed uniformly scaling the sides of a triangle.
(NOTES: similar triangles moved after this, so revise)
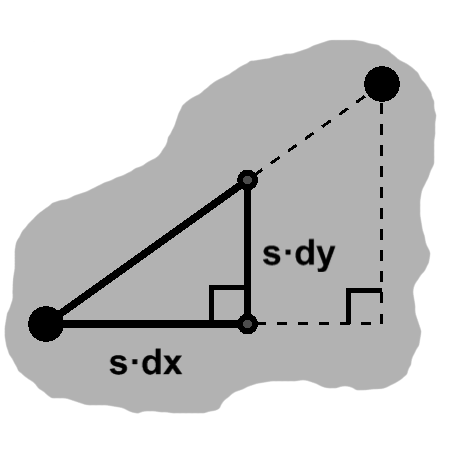
In the case of a right triangle, this is pretty easy. We have two sides of length $dx$ and $dy,$ which we can scale by $s.$ Then the length of the third side would be $ \sqrt{(sdx)^2 + (sdy)^2} = \sqrt{s^2(dx^2 + dy^2)}. $ This simplifies to $ s\sqrt{dx^2 + dy^2}, $ which is exactly what we would expect.
(NOTES: A little too "lucky"; turn the steps around instead)
This applies to triangles in general, but a useful consequence follows when we apply it to distance. Basically, to find the position $s$ of the way along the path between two points, simply scale the two offsets $dx$ and $dy$ by $s,$ then add the results to the original point. This is called linear interpolation.
Importantly, the construction $ a + s(b - a) $ can be rephrased as $ (1 - s)a + sb, $ which is sometimes more convenient.
(NOTES: General triangle could use the implicit lerp triangles)
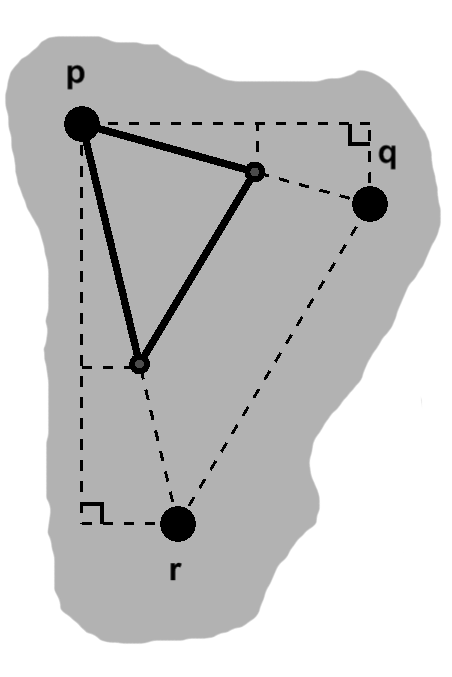
In the more general case, we can choose two of the sides with a common first point and scale them. This is simply the right triangle situation. The third side will depend on the second point, with offsets $ dx_2 = r_x - q_x, dy_2 = r_y - q_y,$ and length $ \sqrt{dx_2^2 + dy_2^2}. $
The second points on this scaled triangle will be at $ \vcomps{(1 - s)p_x + sq_x}{(1 - s)p_y + sq_y} $ and $ \vcomps{(1 - s)p_x + sr_x}{(1 - s)p_y + sr_y}. $ If we find the offsets between these points, the $ 1 - s $ terms cancel and we have $ dx_3 = s(r_x - q_x) $ and $ dy_3 = s(r_y - q_y). $ These are the scalar multiples of $dx_2$ and $dy_2,$ as expected.
(NOTES: More complex than necessary... just split a generic triangle into two right triangles, aligned along the altitude for visual clarity... then to get the two "hypotenuse" sides we scale the legs... since this altitude is a leg of both, we use the same scaling factor, and since s(x + y) = sx + sy, the bases are the same too, so all checks out)
Strikingly similar
Had congruence been the only way to relate two triangles, giving it a special name would be redundant. There is, in fact, another useful concept of "same".
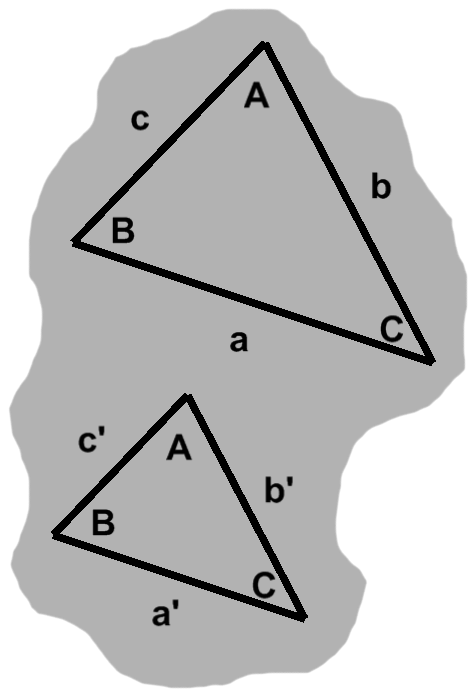
Say we came across the two triangles in figure F-1.
One triangle is visibly smaller than the other, so overlap is clearly not going to happen. That said, both triangles have the same set of angles. In spite of the size difference, the shapes match. (Once we know how to find lengths, we could show that one triangle is simply a scaled version of the other.)
The two triangles are said to be similar.
Similar triangles, like congruent ones, may have different positions and orientations. Two triangles might even share a corner—and thus an angle—so that the smaller triangle is "part of" the larger one, as seen in figure F-2. Naturally, the shared angle would be the same as itself!
(NOTES: For F-3, use variant of F-1; two sides on one of them, one plus a "?" on the other; maybe rotate it for increased generality)
(NOTES: In fact, could strengthen this by swapping with next section; motivate by overlap case and corresponding angles)
(NOTES: Still needs a little finesse to tie in the uniform scaling; perhaps the better-elaborated rigidity section earlier?)
TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE TENTATIVE
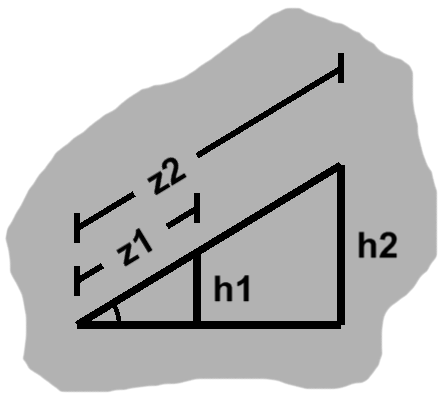
If we scale we have $a^2 + b^2 = s^2z^2,$ whereas the smaller one is $(x - a)^2 + (y - b)^2 = (1 - s)^2 z^2,$ which expands to \begin{align} x^2 + y^2 - 2ax - 2by + a^2 + b^2 & = (1 - 2s + s^2)z^2 \\ & = (1 - 2s)z^2 + s^2 z^2 \\ & = (1 - 2s)(x^2 + y^2) + a^2 + b^2 \\ -2(ax + by) & = -2s(x^2 + y^2) \\ ax + by & = s(x^2 + y^2) \end{align} Collecting this a bit, we have $x(a - sx) + y(b - sy) = 0.$ Since $x$ and $y$ can clearly vary, this must mean that $a = sx$ and $b = sy,$ as suggested by reversing our way through the Pythagorean theorem. So the legs are scaled the same way.
(NOTES: These last two paragraphs give the outline for a more formal establishment of this fact; not sure whether this means swapping the lerp and similarity sections)
(NOTES: That said, simply adjoining triangles to motivate the idea, then using the Pythagorean theorem, gets you most of the way there)
EXERCISES
1. Make an argument for similarity from the midpoint theorem, mentioned in an earlier exercise.
2. If we know two triangles are similar, how can we take of advantage of this by scaling one or both of them? What about rotating? Scaling and rotating? As far as rotation goes, consider that the triangles might be doing so around different centers.
More angle-side postulates
The point about three angles identifying similar triangles is often called angle-angle-angle. In fact, from the triangle postulate, two suffices.
If we have two similar triangles and we find one of the corresponding sides has the same length, it follows that the two triangles have the same scale and are congruent.
Again, we only need two angles to specify a triangle's shape.
These insights give us two more techniques for finding congruent triangles: angle-side-angle and angle-angle-side.
EXERCISES
1. Consider a side-side-angle rule. Could we always rely on this for congruence? Why or why not?
Isosceles triangles: the converse
We saw earlier that, in a triangle where two sides have the same length, these sides were opposite congruent angles. The obvious follow-up question is whether we can go the other way. Given two such angles, what can we say about the sides?
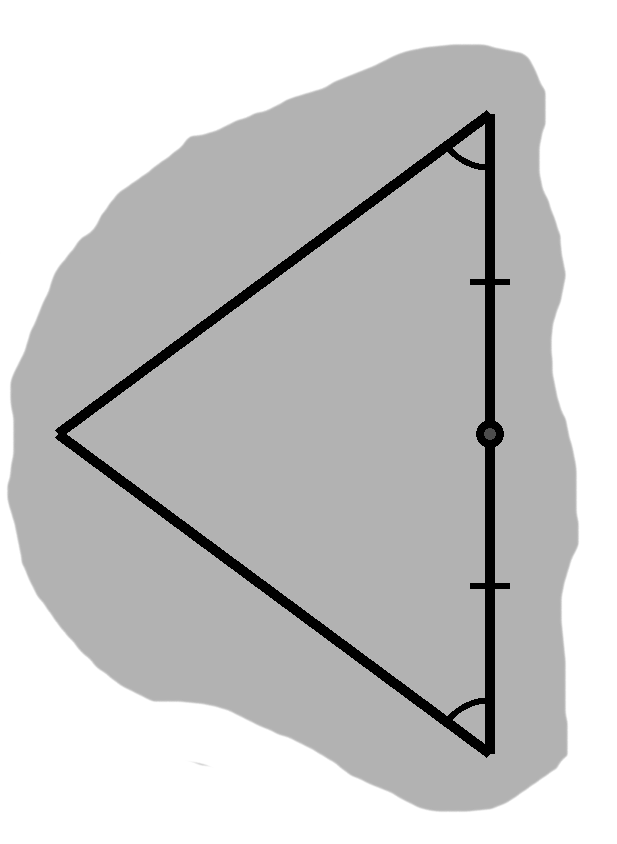
When we studied isosceles triangles before, the third side ended up getting cut in half, on account of the perpendicular bisector. This is as good a place as any to start, giving us the situation in D-1.
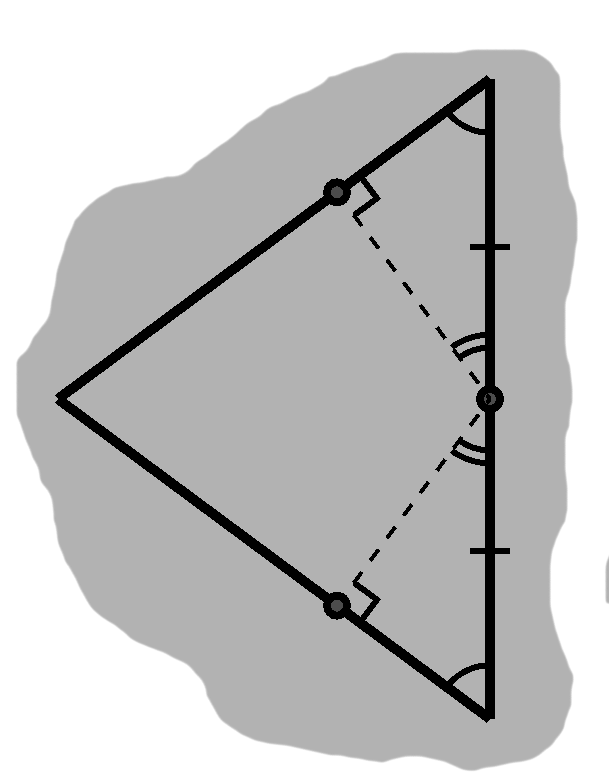
From the midpoint of this third side, we can sketch a couple segments, marked in dashes in D-2, to the other two sides. If we aim these right, we etch out a couple right triangles.
Since we already have know two angles in each case, the third follows. All these angles match, so we also have similar triangles.
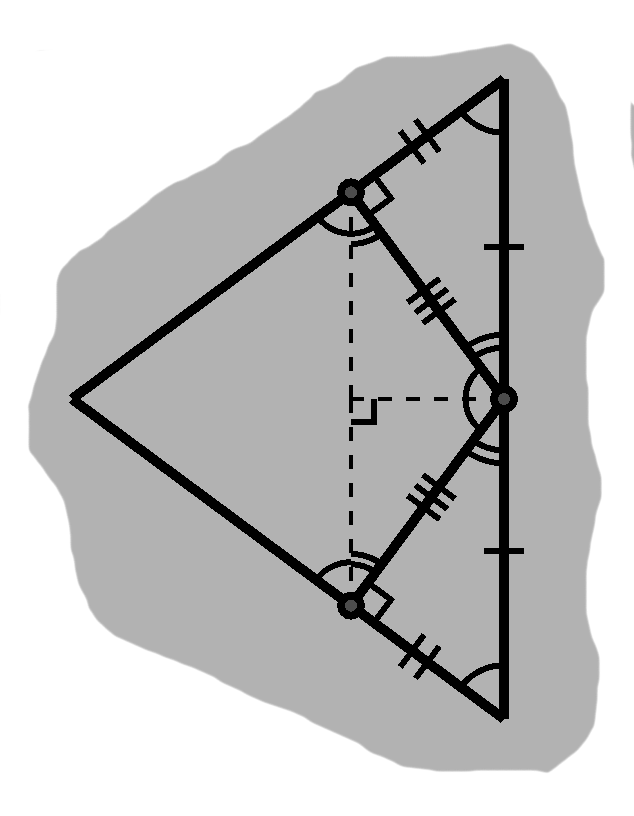
The sides between the one- and two-arced angles both have the same length: the half-side of the original triangle. Thus these right triangles are congruent by either angle-angle-side or angle-side-angle.
We can mark the various sides, as in D-3, to point out the matching side lengths. In particular, we see that if we connect the feet of our two right triangles, we have an isosceles triangle. Since we know these break apart into two right triangles, this new side must be parallel to the side we cut in half in the original triangle. Thus the congruent angles are alternate with the double-arced ones, whereas the bisected parts are complementary to them.
We still have some unexplored bits from the original triangle. The new angles here are complementary to the congruent pair in the isosceles, or corresponding with the original's congruent pair, so match single arcs. Finally, we have D-3.
We can now proceed in a number of ways.
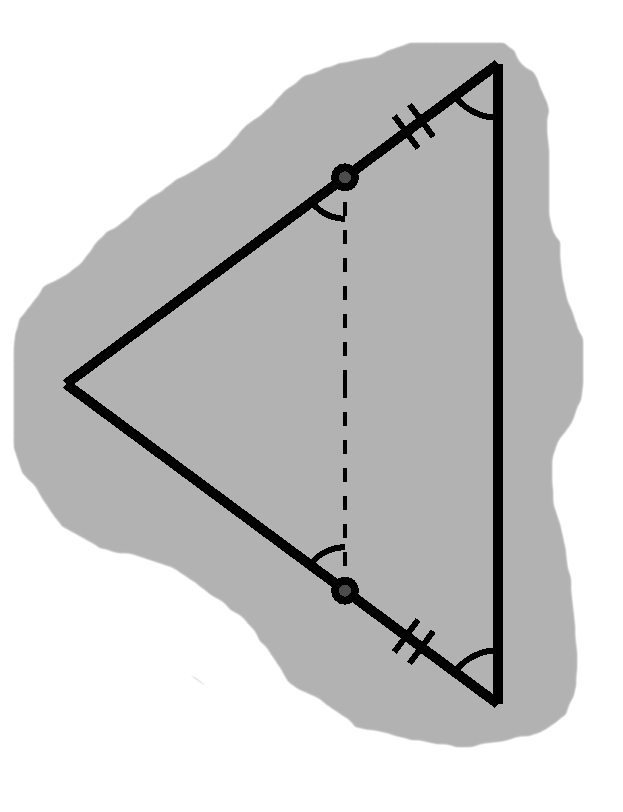
As figure D-4 emphasizes, we have similar triangles, but our two sides will grow by the same amount. So $sa = a + K,$ or $(s - 1)a = K,$ and likewise $(s - 1)b = K,$ thus $a = b.$
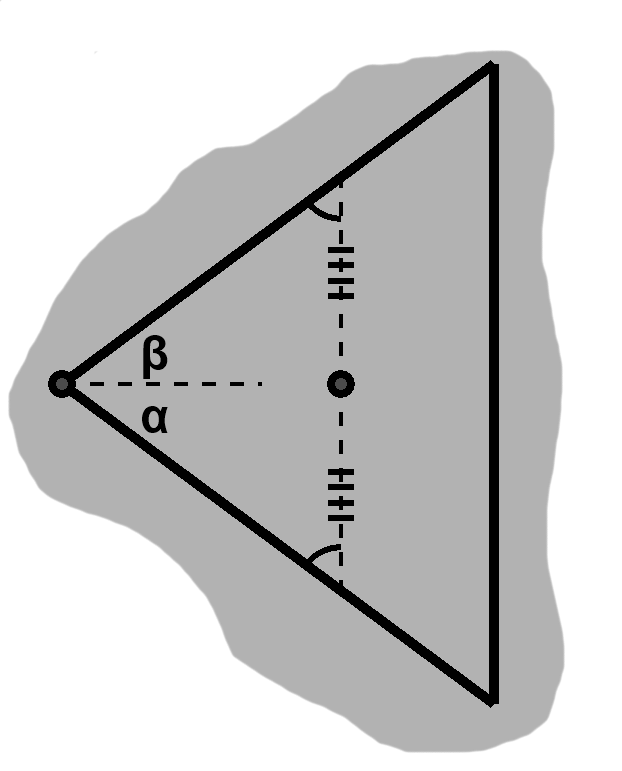
With the approach in D-5, we try cutting the angle in various ways. With $\alpha = \beta$, along with the half-sides of the isosceles and reflexively the side being extended, we have a angle-angle-side configuration.
(NOTES: Mention something about why line is only partial in figure, i.e. experimenting with triangles; mention using side of isosceles?)
(NOTES: Ticks and mark not actually needed here... and in fact we don't know enough to make use of them... relevant to the kite, though)
We get our answer either way: a pair of congruent angles yield congruent opposite sides!
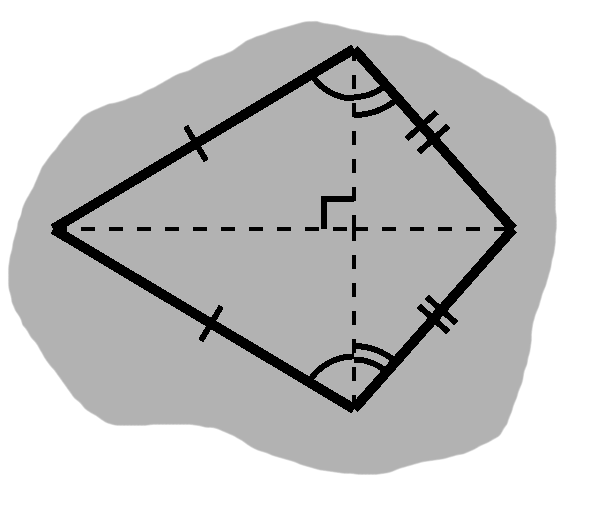
As an aside, the isosceles in this last step and the one from D-3 coincide in their third sides, forming a so-called kite. We will see these occasionally in future articles.
Segments drawn between opposite corners of a kite meet at right angles, as in D-6.
(NOTES: Much smoother than it was, but still needs polish)
EXERCISES
1. Argue for the converse directly from D-1 and angle-side-angle.
2. How else might we reason for the converse from D-4?
Summary
There is much more to be said about triangles. Even so, what we have already is nothing to scoff at. Naturally, the most obvious results, such as which angles are the same and how to measure areas, are important. The assortment of techniques used along the way are also well worth remembering, as they tend to come up again and again.
Future articles will build upon this foundation. Next up: circles!