Today’s guest tutorial comes to you courtesy of X.
Enter Pythagoras
Squares are a special case of rectangles, where all sides have the same length.
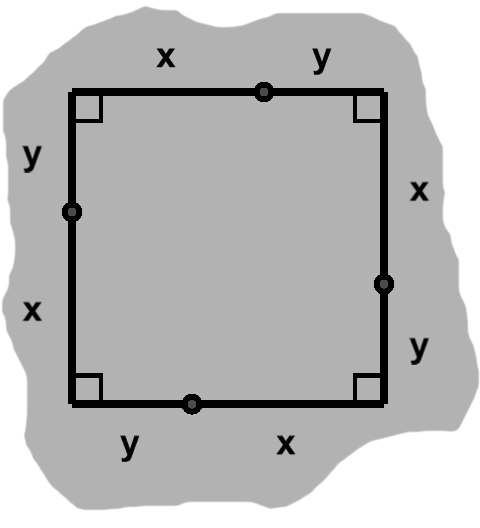
Borrowing an earlier idea, we can divide each of these sides into two lesser lengths, say $x$ and $y.$ If these alternate around the square, we have something like figure J-1.
From the rectangular formula, the total area of the square is $ (x + y) \times (x + y). $ We can expand this to get $ x^2 + 2xy + y^2. $
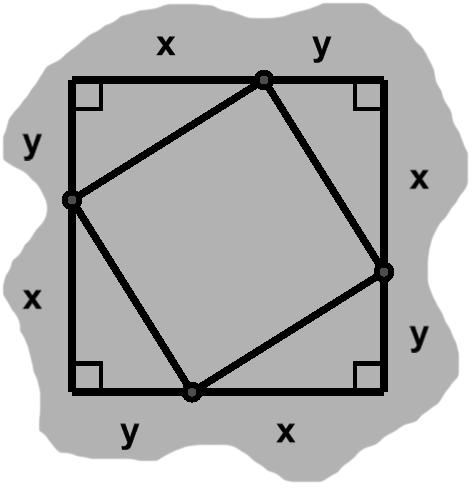
Notice the small nodes in figure J-1, wherever the sides have been split. If we visit these in sequence, drawing segments from one to the next, we etch four right triangles out of the square.
By side-angle-side, we know these triangles are congruent, each with area $ {xy \over 2}. $ The area of all four together is $ 4\left({xy \over 2} \right) = 2xy. $
We can find the area of the middle region—what would remain, if we removed the triangles—by subtracting this sum from the total area of the square. The $ 2xy $ terms cancel, leaving us with $ x^2 + y^2. $
One side of each triangle remains unknown. Owing to congruence, however, these sides all have the same length. We can give them a common label, say $z.$
The middle object's angles each lie along a side of the square; when combined with their neighbors, they form straight lines. Thus, if $A$ and $B$ are the adjacent measurements, a given angle has measure $ 180^{\circ} - A - B $.
As the arcs in J-3 indicate, $A$ and $B$ will be the same in all four cases. The interior angles must therefore be equal as well, measuring $ 360^{\circ} / 4 = 90^{\circ}. $
The middle region is an equal-sided object with four right angles. This is simply a rotated square, with area $ z^2 $. A few paragraphs ago, we described this same area using another formula. We can combine the two, giving us $ x^2 + y^2 = z^2. $
This is the celebrated Pythagorean theorem.
"This base is too short..."
Now, while the central square was key to arriving at this result, the equation actually describes a relationship among triangle sides.
These happened to be right triangles during our derivation, but is this necessary? Might the formula extend to triangles in general, as with area and interior angle sums?
We run into problems right out of the gate. Without a right angle, nothing seems to distinguish any one side. Which one gets to be $z$?
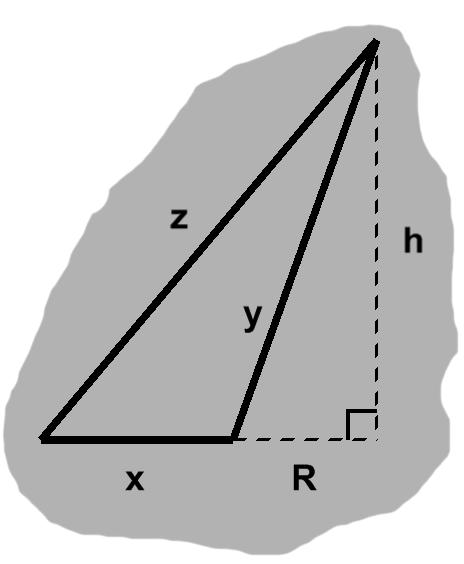
Setting such practical concerns aside, consider the following candidate, depicted in figure K-1. If its base, $x,$ were somewhat wider, we would indeed have a right triangle. As is, it falls short.
We ran across a similar predicament with areas involving obtuse angles. Once again, we can start with the "hypothetical" right triangle that a longer $x$ would give us. This has base $ x + R $ and height $h.$ Of course, it does adhere to the Pythagorean equation: $ (x + R)^2 + h^2 = z^2. $
Also familiar: the added-on part is itself a right triangle. In figure K-1, its legs correspond to the dashed segments. Thus, $ h^2 = y^2 - R^2. $
We can plug this into the previous equation. Following some expansion and cancellation, we have $ z^2 - x^2 - 2xR = y^2. $
Now, if our non-right triangle does indeed satisfy Pythagoras's equation, $ x^2 + y^2 $ will be the same as $ z^2, $ so we can substitute one for the other in the last result. A short bout of cancellation ensues and leaves us with $ -2xR = 0. $
This could mean $ R = 0 $: nothing needs to be added to $x$, so we have a right triangle after all!
Otherwise, $ x = 0. $ This is indeed suspicious.
"...this base is too long..."
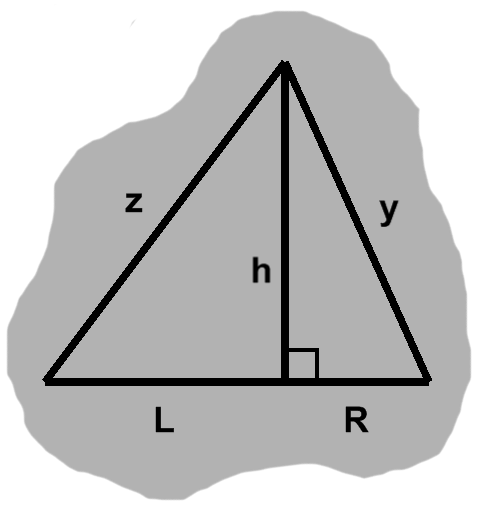
The base might instead be too wide to be a right triangle, as seen for instance in figure L-1.
Delving once more into earlier techniques, we can draw an altitude to break this apart into two right triangles, with bases $L$ and $R$ and a common height $h.$ Applying the Pythagorean theorem to these, we find $ L^2 + h^2 = z^2 $ and $ R^2 + h^2 = y^2. $
Again, assuming the original triangle does satisfy the Pythagorean theorem, we can replace $ z^2 $ in the first equation with $ x^2 + y^2. $ Doing so, then combining the two equations on account of the common $ h^2, $ and finishing off with some cancellation, we end up with $ x^2 + R^2 = L^2. $
Since $ x = L + R, $ this finally boils down to $ 2R(L + R) = 0. $ Either $ L = -R, $ which can only happen when $ x = 0, $ or $ R = 0. $ These are exactly the situations a too-short base gave us, with the same consequences.
"...this one is just right."
The same analysis applies to $y,$ with comparable results. In short, either the solution outright demands a right triangle, or one of $x$ or $y$ must be zero. What do these latter possibilities mean?
When $x$ is zero, the equation reduces to $ y^2 = z^2, $ or $ y = \pm z. $ Similarly, with $y$ we arrive at $ x = \pm z. $ These are simply lines.
Figure M-1 gives us some hint that lines are not a drastic break from the triangular mold. So long as we have a right angle, all is well, even as the height dwindles and our triangle becomes little more than a sliver. A line segment can be understood as going just a bit further, so the height (or width of the base) is zero.
(NOTES: Perhaps a little numerical note, e.g. when $x$ is 1/1000, $x^2$ is 1/1000000, etc. so graceful transition)
So, given $x$, $y$, and $z$ satisfying the Pythagorean theorem, we know these do entail a right triangle, or might as well.
EXERCISES
1. What if $x$ and $y$ both go to zero?
2. How long can the hypotenuse be, compared to its legs?
Going the distance
All well and good, but what do we gain from the theorem?
Basically, knowing how long two sides of a triangle are, we can find the third as well. The hypotenuse is the most obvious choice: $ z = \sqrt{x^2 + y^2}. $ If we already know $z,$ we can find one of the leg lengths instead, say $ x = \sqrt{z^2 - y^2}. $ (Negative roots are irrelevant.)
Consider the two points depicted in figure N-1.
Both can be described by a coordinate pair: $ \vcomps{p_x}{p_y} $ for $ \mathbf{p} $ and $ \vcomps{q_x}{q_y} $ for $ \mathbf{q}. $ Given some point of reference, the $x$- and $y$-coordinates tell us how far to the right of and above it these points are found. For example, $ (1, -3) $ would be one unit to the right and three units below.
Rather than travel in a straight line from one point to the other, we can start from $ \mathbf{p} $ and head right, eventually putting us directly beneath $ \mathbf{q}. $ From there, going straight up will get us the rest of the way.
To perform these intermediate steps, we need to know "Relative to $ \mathbf{p}, $ how much farther to the right and above is $ \mathbf{q} $?". The coordinate differences express exactly this: $ dx = q_x - p_x $ and $ dy = q_y - p_y. $
Taken together, these shorter paths are the legs of a right triangle, as seen for instance in figure N-2. Its hypotenuse is the segment from $ \mathbf{p} $ to $ \mathbf{q}. $ Finding the length of this side will give us the straight-line distance between the two points: $ \sqrt{dx^2 + dy^2}. $