Today’s guest tutorial comes to you courtesy of X.
TODO!
Laws and rights (G)
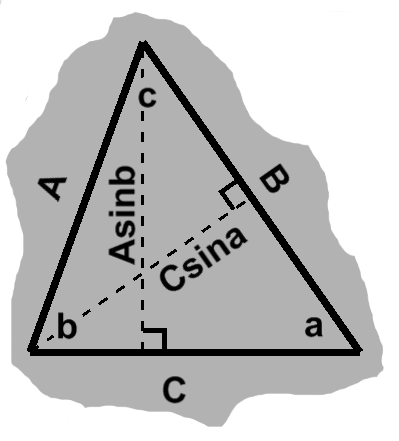
As we have now seen a few times, sine is the key to finding altitudes' heights, in combination with a side as hypotenuse.
Together with the adjacent side, we can find the area of the triangle, say as $ \frac{AC\sin b}{2}. $ (The use of lowercase Latin letters here is conventional and deliberate, with angles opposite sides designated by the uppercase of the same.)
Now, of course, the triangle will have the same area regardless, so choosing another pair of sides and included angle will yield the same result. Thus
\begin{align} \frac{BC\sin a}{2} = \frac{AC\sin b}{2} = \frac{AB\sin c}{2} \end{align}
If we divide "both" sides by ${1 \over 2}ABC,$ this all comes out to
\begin{align} \frac{\sin a}{A} = \frac{\sin b}{B} = \frac{\sin c}{C} \end{align}
This is the Law of Sines, which brings similar power to sines as the previous law did to cosines. (Sometimes the inverse form is used, with $ \frac{B}{\sin b} $ and so on. Since these are intended to relate sides, either way will serve.)
Law of Tangents
We may calculate any altitude in terms of two different side-angle pairs. In G-2, for example, $A\sin b = B\sin a = H,$ where $H$ is the common height.
Some simple restructuring gives us $\sin a = \frac{H}{B}$ and $\sin b = \frac{H}{A}.$
We can bring the sum-to-product identities to bear on these: \begin{align} 2\cos\left(\frac{a + b}{2}\right)\sin\left(\frac{a - b}{2}\right) & = H(\frac{1}{B} - \frac{1}{A}) \\ & = \frac{H}{AB}(A - B) \\ 2\sin\left(\frac{a + b}{2}\right)\cos\left(\frac{a - b}{2}\right) & = \frac{H}{AB}(A + B) \end{align} When we divide one by the other, $\frac{H}{AB}$ goes away. We obtain the Law of Tangents: \begin{align} \frac{A - B}{A + B} = \frac{\tan\frac{a - b}{2}}{\tan\frac{a + b}{2}} \end{align} (NOTES: Can probably merge these two into one "Laws" section; a bit of tightening and rewording is also in order)
Centroid
If we start at one corner and cut the opposite side at the midpoint, we have two triangles with base ${B \over 2}$ and height $h$, which is to say they have equal area, half that of the full triangle. Such lines are called medians.
(NOTES:Figure)
If we do the same with another corner, the same area situation will happen. Furthermore, of course, the medians will intersect somewhere. This will produce a number of triangles.
(NOTES:Refer to figure)
With the Law of Sines we can investigate the relationships among their sides, tabulated in what follows. Note that, as we saw in the previous article, $\sin(180^\circ - \theta) = \sin\theta.$
First off, we have the triangles produced when the two medians cross. These correspond to the upper-left, upper-right, and lower-left triangles in (FIGURE): \begin{align} T_{ul}: \frac{\sin x}{A} & = \frac{\sin b_1}{D} = \frac{\sin c_1}{F} \\ T_{ur}: \frac{\sin x}{B / 2} & = \frac{\sin (x + c_2)}{D} = \frac{\sin c_2}{G} \\ T_{ll}: \frac{\sin x}{C / 2} & = \frac{\sin b_2}{E} = \frac{\sin (x + b_2)}{F} \end{align} The median bisecting $B$ gave us a left and right triangle: \begin{align} Left: \frac{\sin c}{F + G} & = \frac{\sin b_1}{B / 2} = \frac{\sin (x + c_2)}{A} \\ Right: \frac{\sin b_2}{B / 2} & = \frac{\sin a}{F + G} = \frac{\sin (x + c_2)}{C} \end{align} Likewise, from cutting side $C$ we have top and bottom triangles: \begin{align} Top: \frac{\sin c_1}{C / 2} & = \frac{\sin b}{D + E} = \frac{\sin (x + b_2)}{A} \\ Bottom: \frac{\sin c_2}{C / 2} & = \frac{\sin (x + b_2)}{B} = \frac{\sin a}{D + E} \end{align} Many of these results above are dead ends; some trial and error will flush them out. Among the useful bits, after some rearrangement: \begin{align} \sin(x + b_2) & = \frac{2A\sin c_1}{C} = \frac{2B\sin c_2}{C} \\ \sin(x + c_2) & = \frac{2A\sin b_1}{B} = \frac{2C\sin b_2}{B} \end{align} We see that $A\sin b_1 = C\sin b_2$ and $A\sin c_1 = B\sin c_2,$ respectively. This next equality, also derived from the list above, will let us apply these insights: \begin{align} \sin x = \frac{A\sin b_1}{D} = \frac{C\sin b_2}{2E} = \frac{A\sin c_1}{F} = \frac{B\sin c_2}{2G} \end{align}
After substituting a couple of numerators, it quickly follows that $D = 2E$ and $F = 2G.$
Thus, our intersection is ${2 \over 3}$ of the way from either corner to the midpoint of its opposite side.
We can intersect either of the first two medians with the remaining one. Once again this happens ${2 \over 3}$ along; the three medians have a common meeting point.
This is known as the centroid. To find its position, we linearly interpolate from any corner to the opposite midpoint: \begin{align} x = {1 \over 3}x_1 + {2 \over 3}\frac{x_2 + x_3}{2} \end{align} The $y$-coordinate is similar. After simplifying: \begin{align} \mathbf{c} = \left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\right) \end{align} Using the altitudes from the centroid onto the three sides, we can find the areas of the three triangles it forms: $\frac{AD\sin c_1}{2}, \frac{CF\sin b_2}{2}, $ and $\frac{BD\sin c_2}{2}.$
We can reuse one of our earlier substitutions here, telling us the first and third are equal.
Another relationship we can pull out of the earlier list is $C\sin b_2 = \frac{2AE\sin c_1}{F}.$ Given this, the second area reduces to $AE\sin c_1.$ Since $E = {D \over 2},$ this is equal to the others.
Each sub-triangle thus occupies ${1 \over 3}$ of the total area. A triangle may be interpreted as an object of uniform density—in Corona, for instance, this describes a triangular polygon with a physics body—so the centroid sometimes goes by the name of barycenter, or "center of weight".
Barycentric coordinates
We may divide the smaller areas by the larger one, giving us three values, say $b_1$, $b_2$, and $b_3$, that sum to one. Some interesting facts follow on this. As before, points "above" a side have positive sign and those "below" negative. Then there are those on the side itself: here the "sign", or rather the value $b_i$, is zero. Consequently, the corresponding triangle vanishes: it has no area.
The point might also fall on two sides: at one of the corners. Another triangle vanishes. Two areas went to zero, so we have something like $ b_1 = b_2 = 0 $ and $ b_3 = 1. $ At each of the corners, one of the values will be one, the others zero.
When only one of the values was zero, with the point somewhere along one of the sides, the two that remain must still sum to one. Because of the situation prevailing at the corners, it seems reasonable that the nearer this point comes to a corner, the closer one $b_i$ will be to one, the other to zero. In other words, these seem to be a sort of weight, describing relative proximity to each corner. In the interior, all $b_i$ are between zero and one, but the idea still holds. Outside the triangle it does as well, though some $b_i$ will not be positive, and "on the side" might mean rather being on its infinite line.
These are barycentric ("center of weight") coordinates. (TODO: image)
These coordinates, where values of one select a corner and reject the others, suggest that a point can be described by a formula such as $ b_1\mathbf{p} + b_2\mathbf{q} + b_3\mathbf{r} $. In doing so, though, we find ourselves adding points, seemingly at odds with our earlier "arithmetic of types" guidelines.
We can see that no such violation takes place by rephrasing a couple of the points using vectors: $ \mathbf{q} = \mathbf{p} + \mathbf{v} $ and $ \mathbf{r} = \mathbf{p} + \mathbf{w}. $ The formula then becomes $ b_1\mathbf{p} + b_2(\mathbf{p} + \mathbf{v}) + b_3(\mathbf{p} + \mathbf{w}) $. After distributing the scale factors, this restructures as $ (b_1 + b_2 + b_3)\mathbf{p} + b_2\mathbf{v} + b_3\mathbf{w} $.
The parenthesized values sum to one, so the "scaling" leaves the point as is. The remaining terms are scaled vectors, which add to points just fine. Barycentric combinations are point-vector sums in disguise. (For that matter, if scaling a point also scales its "type"—making it equal to the scale factor—then although this intermediate result is some alien object, so long as the "types" all sum to one we will again have a point after adding all our pseudo-points together.) (TODO: as footnote?)
Barycentric coordinates are useful in that they allow us to operate in relative terms—near this corner, between these points, somewhere in the center—without needing to know the specifics of the triangle, such as point locations and distance. Interpolation between such coordinates comes quite naturally, as well.
The idea extends to four points, for instance in the assortment of "shape functions" used to decompose meshes into simpler parts. More complex problems are a subject of ongoing research.
(IMAGE: 20)
Summary
Revise!