Today’s guest tutorial comes to you courtesy of X.
TODO!
Laws and rights (G)
When discussing double angles we split a triangle up into two right triangles and made some analysis of the results, with the assumption that the points were either on the unit circle or its center.
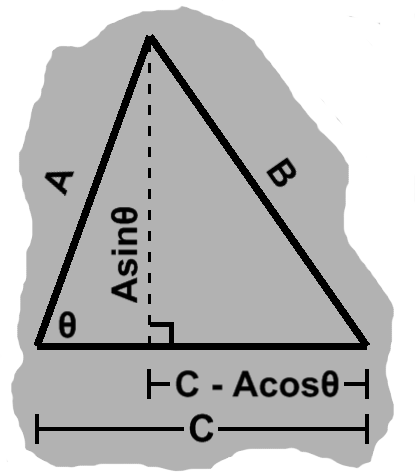
This sort of triangle will also arise in more general circumstances, where some of the details will remain intact. The base of the left-hand triangle, for instance, can usefully be subtracted from the combined base to give the right-hand side.
Then we can apply the Pythagorean theorem on the right-hand side, tying all three sides together in one equation: $ (A\sin\theta)^2 + (C - A\cos\theta)^2 = B^2. $
After expansion, this gives us the so-called Law of Cosines:
\begin{align} A^2 + C^2 - 2AC\cos\theta & = B^2 \end{align}
This gives us a means of using the cosine with non-right triangles. In particular, when we know a couple of sides and one of the angles, we can find the (squared) length of the third side.
Although we generalized away from circle-based triangles, in that case two of the sides will be $r,$ giving us
\begin{align} r^2(2 - 2\cos\theta) & = B^2 \end{align}
This gives us a second chord formula, in this case for the squared length.
(NOTES: Obtuse angles)
(NOTES: Nail down the triangle inequality)
Heron
Choosing one of the equivalent area formulas from the previous section, we can rephrase it in terms of cosine: $\frac{BC\sqrt{1 - \cos^2a}}{2}.$
From the law of cosines, $\cos a = \frac{B^2 + C^2 - A^2}{2BC}.$ After substitution and a bit of arithmetic, we have $\frac{1}{4}\sqrt{4B^2C^2 - (B^2 + C^2 - A^2)^2}.$
We have an area formula that only depends on side lengths. No need for angles or altitudes.
The expression inside the root has the form $X^2 - Y^2,$ so we can factor it as $(X + Y)(X - Y).$
For the $X + Y$ side, we have $2BC + B^2 + C^2 - A^2.$
We can break up $2BC$ up into $BC + BC,$ then pair one off with $B^2$ and the other with $C^2,$ after which we can pull out a common $B$ and $C,$ respectively: $B(B + C) + C(B + C) - A^2.$ Furthermore, we can group these first two terms: $(B + C)^2 - A^2.$ At this point, we have something we can factor again, giving us: $(B + C - A)(B + C + A).$
The expression on the right, $p = A + B + C,$ is the perimeter of the triangle. We would also get the perimeter if we added $2A$ to our left-hand expression. Altogether, then, we have $p(p - 2A).$
The $X - Y$ side has the form $2BC - B^2 - C^2 + A^2$. Following the same procedure, we end up with $(p - 2B)(p - 2C).$
After substituting back into our root, we now have our area phrased as $\frac{1}{4}\sqrt{p(p - 2A)(p - 2B)(p - 2C)}.$ We can bring the constant back inside the root as $\frac{1}{16}.$ Since $16 = 2^4,$ we can dole out $\frac{1}{2}$ to each of the four factors. Finally:
\begin{align} area = \sqrt{s(s - A)(s - B)(s - C)} \end{align}
(Here, $s = \frac{1}{2}p,$ the so-called semiperimeter.) This is Heron's formula (sometimes Hero's).
Orthocenter (A)
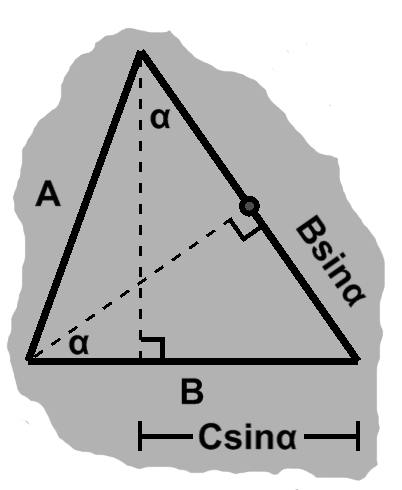
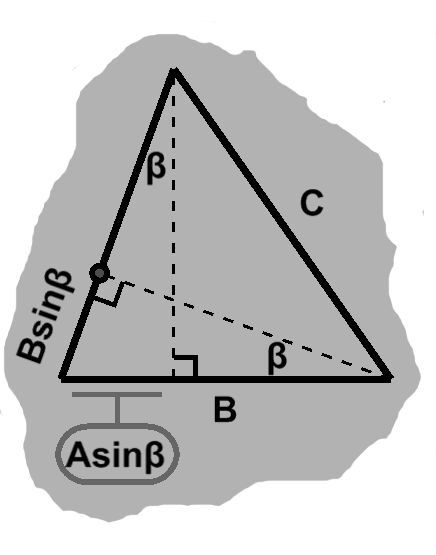
Now, we see that two altitudes will cross, forming new triangles. When we align one of the sides horizontally, one altitude will come down the middle and the other along the side. This is the sort of geometry we encountered during angle addition, causing the angle of the cut to propagate up top. Depending on our choice of second altitude, we will have the left- or right-hand situation.
Now, both cases have the same altitude in common, so $ B = A\sin\beta + C\sin\alpha, $ and also $ A\cos\beta = C\cos\alpha. $
From what we saw earlier, we can find the height of the intersection in each case. On the left, $ A\sin\beta\tan\alpha, $ and on the right, $ C\sin\alpha\tan\beta. $
Now, of course, because of the duplicated angles, we have $ \tan\alpha. $ From the definition, this is $ \frac{C\sin\alpha}{C\cos\alpha}, $ the legs of the right-hand triangle in the left image.
Furthermore, because of the common altitude, we can substitute $ A\cos\beta $ into the denominator. We then have $ A\sin\beta\left(\frac{C\sin\alpha}{A\cos\beta}\right), $ which regroups as $ C\sin\alpha\tan\beta. $
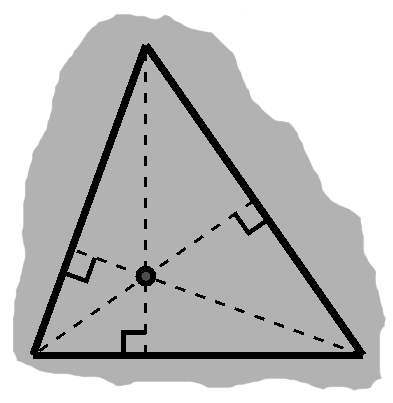
But this is exactly the height of the other intersection! In the end, the altitudes all meet in a single point, called the orthocenter.
Of occasional interest, we can connect the feet to get the orthic triangle.
We can see how to interpolate to the various feet. Along the bottom, one base is $ A\sin\beta, $ so the fraction is $ \frac{A\sin\beta}{B}. $ Similarly, along the other sides we have $ \frac{B\sin\beta}{A} $ and $ \frac{B\sin\alpha}{C}. $
Now, from the law of cosines, $ B^2 = A^2 + C^2 - 2AC\cos(\alpha + \beta). $ We may group the evaluated cosine as $ (A\cos\beta)(C\cos\alpha) - (C\sin\alpha)(A\sin\beta). $ Some substitutions turn this into $ A^2\cos^2\beta - (B - A\sin\beta)(A\sin\beta), $ further reducing to $ A^2 - AB\sin\beta. $ Plugging this back in and performing some further rearrangement, we have
\begin{align} A^2 + B^2 - C^2 = 2AB\sin\beta \end{align}
We have $ \sin\beta $ expressed completely in terms of our side lengths! These are hard numbers we can quickly solve, then plug into several of the equations above.
The value of $ \sin\alpha $ quickly follows from the substitution $ \frac{B - A\sin\beta}{C}. $
From here, we can find each of the feet. Given this, we can find the length of our central altitude, giving us the cosines in turn. From these we can evaluate one of the tangents and use it to solve for the orthocenter height.
In code, this would be:
function Orthocenter ( px, py, qx, qy, rx, ry, want_orthic_triangle )
-- Deltas for sides A, B, C.
local ax, ay = qx - px, qy - py
local bx, by = rx - px, ry - py
local cx, cy = qx - rx, qy - ry
-- Squared side lengths.
local A2 = ax^2 + ay^2
local B2 = bx^2 + by^2
local C2 = cx^2 + cy^2
-- Find the foot of the altitude on side B. From there, walk up the altitude (we will be
-- moving toward point q) until we reach the orthocenter.
-- sin(beta) = (A2 + B2 - C2) / (2 * A * B)
local bt = .5 * (A2 + B2 - C2) / B2 -- (A * sin(beta)) / B
local fx, fy = px + bt * bx, py + bt * by
local ABSinB, ASinB_2 = B2 * bt, B2 * bt^2 -- A * B * sin(beta); (A * sin(beta))^2
local h2 = A2 - ASinB_2 -- height = A * cos(beta), which equals C * cos(alpha)
local ht = (ABSinB - ASinB_2) / h2 -- (A * sin(beta) * tan(alpha)) / (A * cos(beta))
local ox, oy = fx + ht * (qx - fx), fy + ht * (qy - fy)
-- If requested, get the orthic triangle's corners too.
if want_orthic_triangle then
local at = ABSinB / A2 -- (B * sin(beta)) / A
local ct = (B2 - ABSinB) / C2 -- (B * sin(alpha)) / C
return ox, oy, {
a = { x = px + at * ax, y = py + at * ay },
b = { x = fx, y = fy },
c = { x = rx + ct * cx, y = ry + ct * cy }
}
end
return ox, oy
endCuriously, the three original points and the orthocenter together form an orthocentric tetrad. If we take the orthocenter of three of them, we will get the odd one out in return. For instance, $ \mathbf{p}, $ the orthocenter, and $ \mathbf{r} $ will yield $ \mathbf{q} $ back as new orthocenter.
Trilinear Coordinates
So far, there seems to be a relationship of sorts between a center and its altitudes.
We saw above how angles $\alpha$ and $\beta$ showed up in a couple places when the full altitudes crossed. In either case the triangle pair has a vertical angle in common. We can bring the law of sines into play, for instance with $\beta$: \begin{align} \frac{\sin({\pi \over 2} - \beta)}{C\cos a} = \frac{\sin\beta}{B'} \end{align} and \begin{align} \frac{\sin({\pi \over 2} - \beta)}{C\cos b} = \frac{\sin\beta}{A'} \end{align} from which we can deduce that $A'\cos a = B'\cos b.$
The perpendiculars have lengths $A' = C\cos b\tan\beta, B' = C\cos a\tan\beta,$ and $C' = A\cos b\tan\alpha.$
From inspection, we see $\tan\alpha = \frac{\cos a}{\sin a}$ and $\tan\beta = \frac{\cos c}{\sin c}.$ So $A' = \frac{C}{\sin c}\cos b\cos c$ and $C' = \frac{A}{\sin a}\cos a\cos b.$
From above, $B' = \frac{A'\cos a}{\cos b}.$ This further expands as $\frac{C}{\sin c}\cos a\cos c.$
(NOTES: Law of sines not yet available, just use substitution)
(NOTES: Use two cosines version first, then allow secant as alternative)
From the law of sines we know the fraction out front is common in all cases. We could also "un-cancel" the product of cosines, giving us a common factor $k = \frac{A}{\sin a}\cos a\cos b\cos c.$ We can then express our perpendiculars as $A' = k\sec a, B' = k\sec b,$ and $C' = k\sec c.$
These are known as trilinear coordinates. In the case of the orthocenter, a typical representation would go: \begin{align} k\sec a : k\sec b : k\sec c \end{align} This is ratio notation, meant to convey that we care about the relative relationships of the sides. Importantly, this means the $k$ can be any non-0 value and tell us the same thing. Often it will be 1 and omitted.
(NOTES: Generalize)
EXERCISES
1. Find trilinear coordinates for the centroid. What mechanism do these describe, under the aforementioned physical interpretation of a triangle?
2. Write a Lua function to get a position, given a triangle's points and a trilinear coordinate triple.
Summary
Revise!