A 2D geometry primer, extra 2: the incircle

Today’s guest tutorial comes to you courtesy of X.

We might also try to find a circle inside a triangle.

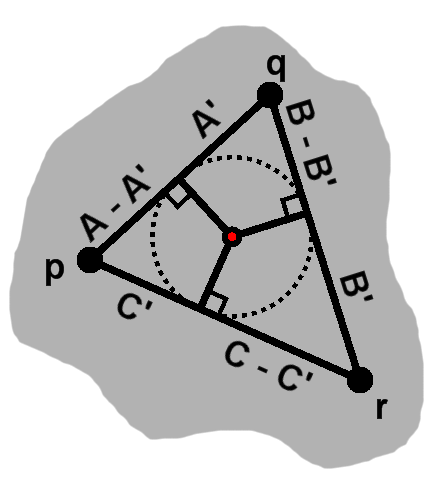
Presumably we would only want it to touch the sides, which would mean these are tangent to the circle at those points. Thus each segment from the center is perpendicular to the side.

C-1

These segments will all have radial length, of course. So we may slice out an isosceles triangle thus. Doing so will also carve out a second triangle.

This triangle has angles complementary to those of the first. Thus, it also happens to be an isosceles.

A-2

Thus, between these two side points we have a radical axis.

Now, we can split this triangle in half and concentrate on a right triangle. Its hypotenuse is the distance of the side point from $ \mathbf{q}. $ We can call this $ A' $ with $A$ itself as the distance from $ \mathbf{p} $ to $ \mathbf{q}. $ Then $ A - A' $ is the other length.

This situation prevails on each side, so we find lengths $ B, B', C, $ and $C'$ as well.

Now, because of the isosceles, we have $ A' = B - B'. $ Likewise, $ B' = C - C' $ and $ C' = A - A'. $

By substitution, $ A' = B - (C - C') $ and further $ A' = B - (C - (A - A')), $ or $ 2A' = A + B - C. $ Finally, $ A' = \frac{A + B - C}{2}. $ Plugging this back in, we get $ B' = \frac{B + C - A}{2} $ and $ C' = \frac{A + C - B}{2}. $

The first side point is $ A' \over A $ of the way from $ \mathbf{q} $ back to $ \mathbf{p}. $ Similarly, we can interpolate the other points.

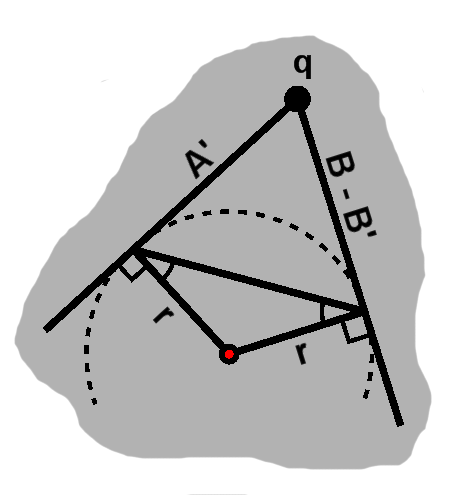
At this point, we have three points with an implicit underlying triangle exhibiting the arc behavior from before, so it would actually suffice to find their circumcircle. Nevertheless, it is worth using the situation at hand.

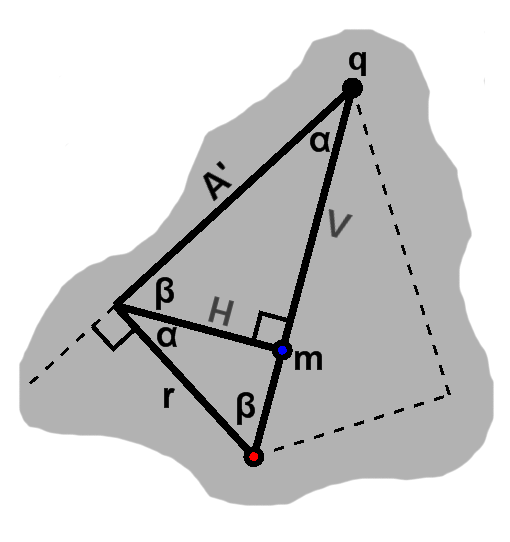
Returning to the right triangle, let us find its leg lengths. The triangle's corners consist of one side point, its midpoint with another, and $ \mathbf{q}. $ We can easily take their lengths, giving us $ A'\cos\beta = \sqrt{(m_x - x_1)^2 + (m_y - y_1)^2} $ and $ A'\sin\beta = \sqrt{(q_x - m_x)^2 + (q_y - m_y)^2}. $ For clarity, call these roots $H$ and $V$ for horizontal and vertical, respectively.

A-3

Now, we know $ \alpha + \beta = 90^{\circ}. $ This lets us put those in the other slots in the larger right triangle and tells us that $ r = A'\tan\alpha. $

A-4

From the geometry we see that $ \cos\alpha = \sin\beta $ and $ \sin\alpha = \cos\beta, $ thus $ \tan\alpha = \frac{H / A'}{V / A'}, $ and $ r = A'\frac{H}{V}. $

To find the center, we want to follow $ \mathbf{q} $ to the midpoint $ \mathbf{m}, $ then push on a little farther.

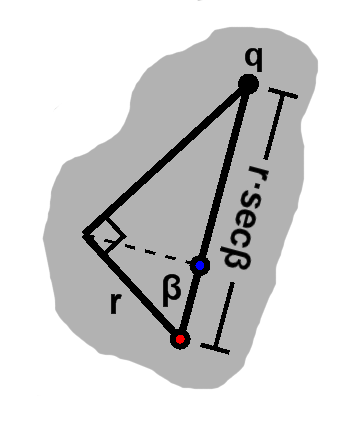
That longer distance is the hypotenuse of the right triangle, so it has length $ r\sec\beta. $ We see elsewhere that $ A' = H\sec\beta. $ After adding our above result for $r,$ the length is $ \frac{(A')^2}{V}. $ We want its ratio to $V,$ of course, so the final scale factor is $ \left(\frac{A'}{V}\right)^2. $

Our center quickly follows from this. Again in code:

local sqrt = math.sqrt

function Incircle ( px, py, qx, qy, rx, ry, want_contact_triangle )
  -- Side lengths.
  local A = sqrt( (qx - px)^2 + (qy - py)^2 )
  local B = sqrt( (rx - qx)^2 + (ry - qy)^2 )
  local C = sqrt( (px - rx)^2 + (py - ry)^2 )

  -- Partial side lengths.
  local Ap = (A + B - C) / 2
  local Bp = (B + C - A) / 2

  -- Find a couple contact points.
  local a1, b1 = Ap / A, Bp / B
  local a2, b2 = 1 - a1, 1 - b1
  local x1, y1 = a1 * px + a2 * qx, a1 * py + a2 * qy
  local x2, y2 = b1 * qx + b2 * rx, b1 * qy + b2 * ry

  -- Get the midpoint between them. The midpoint is along the way from the corner shared
  -- by the two sides, i.e. q, to the center. Evaluate this partial route.
  local mx, my = (x1 + x2) / 2, (y1 + y2) / 2
  local hx, hy = mx - x1, my - y1
  local vx, vy = mx - qx, my - qy

  -- Together, one of the contact points, the midpoint, and q describe a right triangle.
  -- Get its leg lengths, the "horizontal" and "vertical" distances.
  local H2, V2 = hx^2 + hy^2, vx^2 + vy^2

  -- Find the radius.
  local scale = Ap^2 / V2 -- q-to-center : q-to-midpoint = r * sec(beta) / V = (A' / V)^2
  local r = sqrt(H2 * scale) -- r = A' * tan(alpha)

  -- Scale the direction found earlier. Walk along it from q to reach the center.
  local cx, cy = qx + scale * vx, qy + scale * vy

  -- If requested, find the third, otherwise-redundant contact point and supply the triangle.
  if want_contact_triangle then
    local Cp = (A + C - B) / 2
    local c1 = Cp / C
    local c2 = 1 - c1
    local x3, y3 = c1 * rx + c2 * px, c1 * ry + c2 * py

    return cx, cy, r, {
      a = { x = x1, y = y1 }, b = { x = x2, y = y2 }, c = { x = x3, y = y3 }
    }
  end

  return cx, cy, r
end

EXERCISES

1. What are the incenter's trilinear coordinates?