Today’s guest tutorial comes to you courtesy of X.
On the fringes
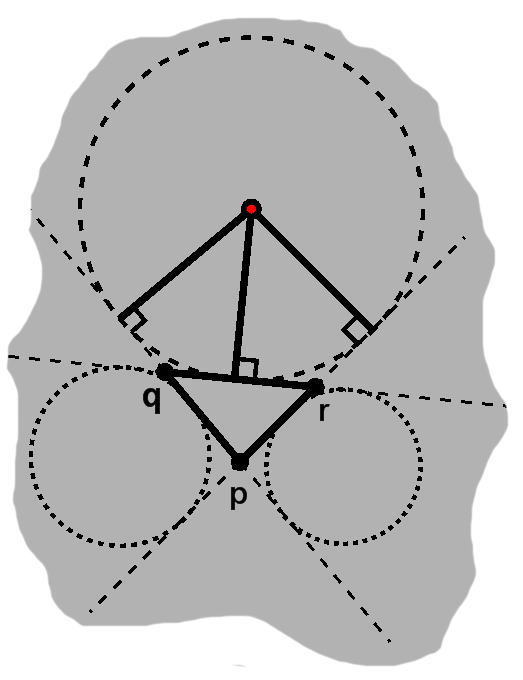
By relaxing our constraints a little, it turns out there are more circles that touch all three sides of a triangle.
The key is that two of these will be extensions of the triangle's sides, so-called sidelines.
Then we have one touch on a true side, two more on these extensions. This is true for each of the triangle's three sides, giving us the excircles.
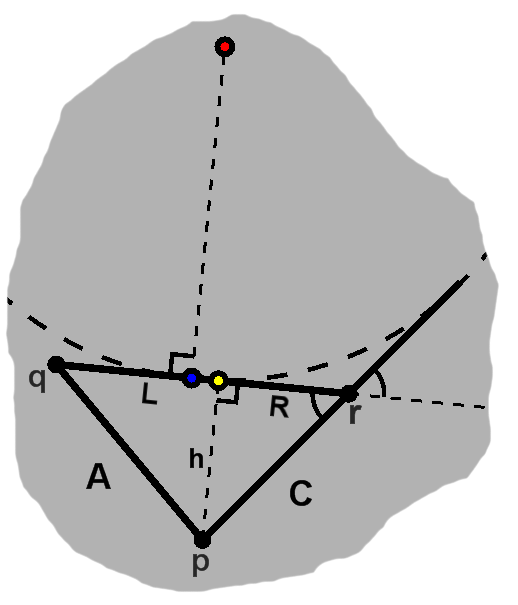
As with the incircle, we begin with the insight that we have radius-length segments emanating from a center, with the circles themselves tangent to the sides.
As can be seen, this will give us a couple adjacent sectors on the circle, grazing the side in question.
Since these are radius-length, part of each sector will be an isosceles triangle. As with incircles, since the common angles were each part of a right angle, the complementary angles also give a second isosceles.
Thus we get the fairly familiar quadrilateral, which we can exploit.
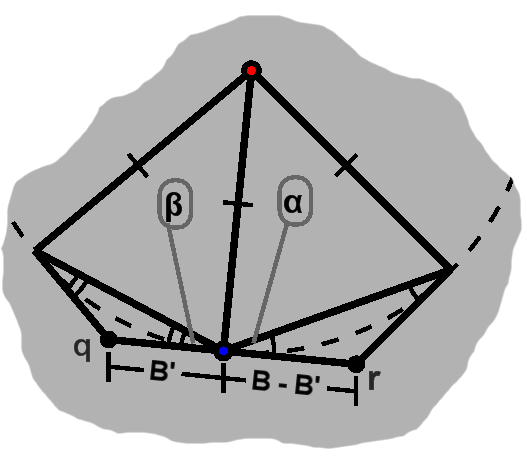
First, since the two angles are the same, we know the remaining one is supplementary to their sum. This in turn tells us that the adjacent angle is valued at their sum.
Importantly, we can go "right" by $ (B - B')\cos 2\alpha, $ then "up" by $ (B - B')\sin 2\alpha, $ to arrive at one of the contact points.
Second, via a combination of the complementarity of the angle and the fact that the midpoint in the quadrilateral occurs at a right angle, we know the angle bubbles up top.
In other words, we have $ r\tan\alpha = B - B'.$ We would get something similar on the left: $ r\tan\beta = B'.$ If we add these together, we have $ r(\tan\alpha + \tan\beta) = B, $ or $ r = \frac{B}{\tan\alpha + \tan\beta}. $
These results apply to both sectors, of course.
Up to this point, we have ignored our triangle's third point, but now can bring it back into play.
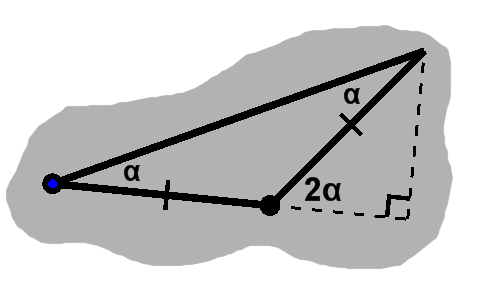
In particular, we have a vertical angle with the previous supplementary angle.
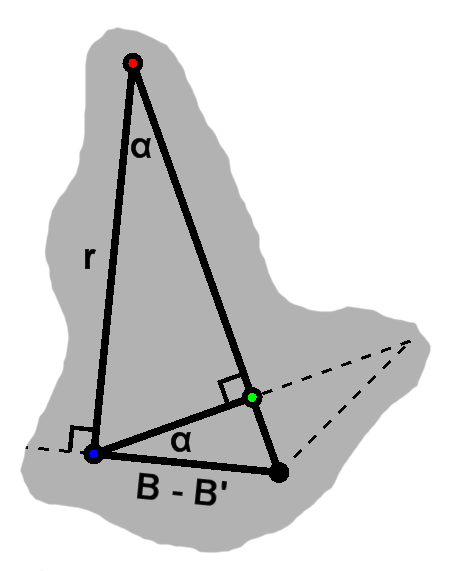
We already saw how to find this foot, where all the points are available, above with the orthocenter. This will split up the side into two parts, $L$ and $R.$ Note that this foot generally differs from that of the excircle center, as in this example.
We can now start plugging in hard numbers.
We know this angle on the right is $ 2\alpha, $ so we have $ \cos 2\alpha = \frac{R}{C}, $ $ \sin 2\alpha = \frac{h}{C}, $ and $ \tan 2\alpha = \frac{h}{R}. $
Now, $ \tan 2\alpha = \frac{2 \tan\alpha}{1 - \tan^2\alpha}. $ We can find the squared term as $ \frac{1 - \cos 2\alpha}{1 + \cos 2\alpha}, $ which with some substitution is $ \frac{C - R}{C}\frac{C}{C + R}. $ Simplifying and subtracting from 1, we end up with $ 2\frac{R}{C + R} $ in the denominator.
We already have our result for $ \tan 2\alpha, $ so we can plug that back in and rearrange everything in terms of $ \tan\alpha. $ In the end we have $ \tan\alpha = \frac{h}{C + R}. $ Finding $ \tan\beta $ proceeds similarly, albeit with $A$ and $L.$
With these, $r$ follows immediately, then $B',$ giving us our middle foot.
From there we can scale the middle segment and go up to find the remaining contact points.
(NOTES: ROUGH! Need to find best way to work in all the angles and points... but already better)
In code, it will go something like:
local sqrt = math.sqrt
local function DoExcircle ( px, py, qx, qy, rx, ry, circles, contacts, extouch, side )
-- Deltas for sides A, B, C.
local ax, ay = qx - px, qy - py
local bx, by = rx - px, ry - py
local cx, cy = qx - rx, qy - ry
-- Squared side lengths.
local A2 = ax^2 + ay^2
local B2 = bx^2 + by^2
local C2 = cx^2 + cy^2
-- Using the orthocenter approach, find the offset of the foot of q on segment pr, as
-- well as the height of the associated altitude.
local bt = .5 * (A2 + B2 - C2) / B2
local h = sqrt( A2 - B2 * bt^2 )
-- Side lengths.
local A = sqrt( A2 )
local B = sqrt( B2 )
local C = sqrt( C2 )
-- Break the pqr triangle into two right triangles at the foot and use this to find angle
-- information shared by the excircle. This will give us the radius.
local L, R = bt * B, (1 - bt) * B
local TanA, TanB = h / (C + R), h / (A + L)
local kr = 1 / (TanA + TanB)
-- From the radius we can find the foot of the center onto the triangle side. Reaching the
-- center is then simply a matter of walking up the altitude.
local Bp = kr * TanB
local Fx, Fy = px + Bp * bx, py + Bp * by
-- Given the foot and radius, similar triangles will put us at the center.
circles[side] = { x = Fx - kr * by, y = Fy + kr * bx, r = B * kr }
-- If requested, supply the contact triangle and / or one side of the extouch triangle.
if contacts or extouch then
Bp = Bp * B
local at, ct = Bp / A, (B - Bp) / C
if contacts then
contacts[side] = {
a = { x = px - at * ax, y = py - at * ay },
b = { x = Fx, y = Fy },
c = { x = rx - ct * cx, y = ry - ct * cy }
}
end
if extouch then
extouch[side] = { x = Fx, y = Fy }
end
end
end
function Excircles ( px, py, qx, qy, rx, ry, want_contact_triangles, want_extouch_triangle )
local contacts, extouch = want_contact_triangles and {}, want_extouch_triangle and {}
local circles = {}
DoExcircle( px, py, qx, qy, rx, ry, circles, contacts, extouch, 1 )
DoExcircle( qx, qy, rx, ry, px, py, circles, contacts, extouch, 2 )
DoExcircle( rx, ry, px, py, qx, qy, circles, contacts, extouch, 3 )
return circles, contacts, extouch
end(NOTES: In that same bit of code, the stuff in comments is following the material in the section, whereas the code itself is jumping the gun... or rather using the tangent logic from the circles section... make this clear)
EXERCISES
1. Find trilinear coordinates for each excenter.
Circles all the way down
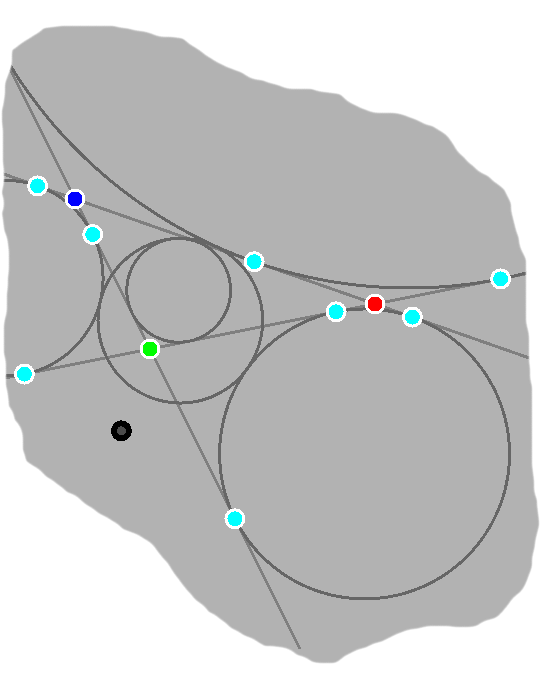
Yet another circle, depicted in B-1, touches all the excircles as well as the incircle, with plenty of other interesting properties as well, while a different circle surrounds them all.
We can keep going with this. The contact triangle, for instance, will have its own circumcircle, incircle, excircles, and the rest. And so on, ad infinitum.
As far as a circle is concerned, these centers and radii are nothing special. However, since they arise on account of a triangle, in a sense they belong to it. Such special points fall under the heading of triangle center. Many of these have interesting properties, as the circumcenter and incenter show. While literally impossible to know all of them, it is good to be aware of them.
(NOTES: Mention Apollonius circle)
Summary
Thus far, our investigations have covered triangles and circles. We have examined many of their properties, such as angles, lengths, and areas, and various facts that follow from them.
The next article will bring vectors into the fold. We will explore new ground, of course, but also build on our many discoveries thus far.