A 2D geometry primer, extra 1: the circumcircle

Today’s guest tutorial comes to you courtesy of X.

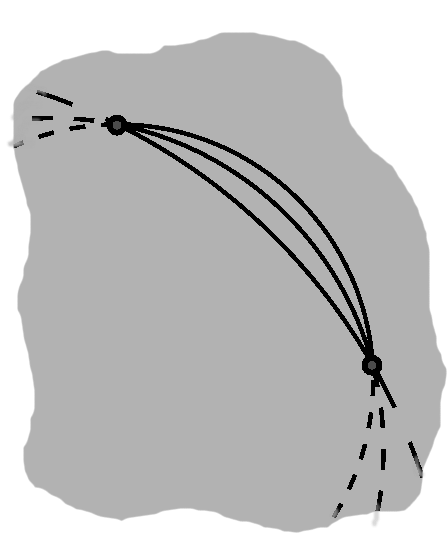
Now that we know about the radical axis, we can turn some of its ideas around.

Given two points with such an axis, a line will run perpendicular to its middle. Somewhere along that line will be the center of a circle, depending on the shape of the arc.

B-1

As this very variety demonstrates, two points alone are unable to pin the center down.

As one choice of center, could be the one that would see the other point also on the circle.

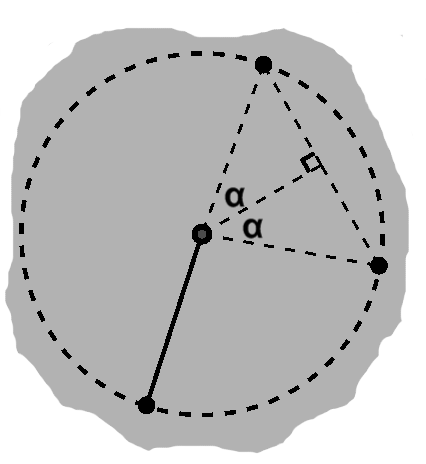
If we had a circle, we could put another point on it somewhere. There would then be two new arcs between this and the original two points. These will naturally have their own radical axes and corresponding perpendicular bisectors.

B-2

As the figure suggests, this immediately constraints a center. (In fact, two arcs are enough to do so, on the unit circle.) For that matter, the bisectors all intersect there.

(TODO: there is good material in these last three, but needs some consistency)

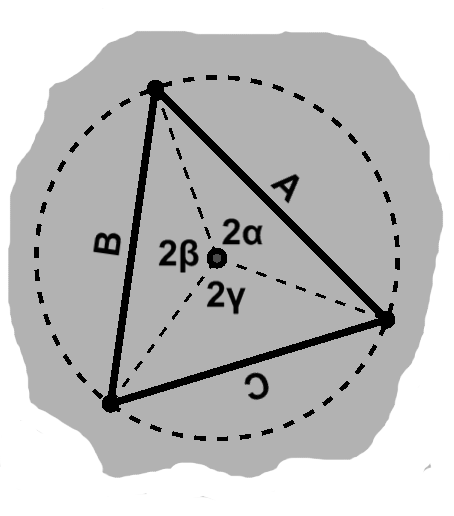
We have a trio of bisected radial isosceles triangles. These will have outer sides of $ 2r \sin\alpha, 2r \sin\beta, $ and $ 2r \sin\gamma $ with those half-angles, respectively.

(NOTES: Law of Sines!)

Now, presumably we know what these three points are. So we can use our length formula to give concrete values to these lengths. Call the above $ A, B, $ and $C. $

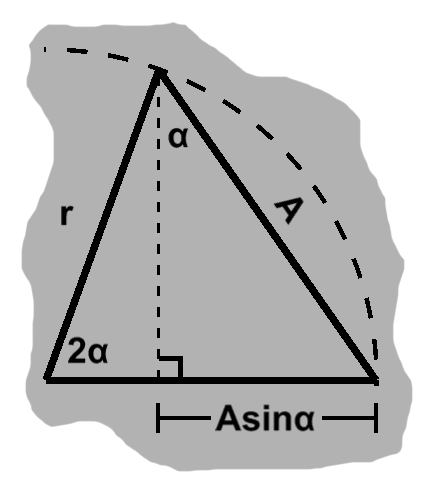
We saw earlier how to break down the structure of a double-angle triangle. So we can express the radius as $ r = r\cos 2\alpha + A\sin\alpha. $ But we know that $ \frac{A}{2r} = \sin\alpha. $ After substitution and some rearrangement, this becomes $ \cos 2\alpha = 1 - \frac{A^2}{2r^2}. $

(TODO: We CAN just pull this from the formula, but might provide more insight)

We can apply this same analysis to the other two triangles.

At this point, it will be helpful to presume we already have our circle and are on it. Thus we want to deal with some local points. For instance, $ \vcomps{x_1}{y_1}, $ where $ x_1 = p_x - c_x $ and $ y_1 = p_y - c_y, $ and likewise for $ \mathbf{q} $ and $ \mathbf{r}. $

From the figure, we can see that these points are simply rotations of one another. So we can express them as such: $ x_2 = x_1\cos 2\alpha - y_1\sin 2\alpha $ and $ y_2 = x_1\sin 2\alpha + y_1\cos 2\alpha. $

B-3

We can use the same strategy from angle differences to simplify this and then add the equations together. Doing so, we wind up with $ x_1 x_2 + y_1 y_2 = (x_1^2 + y_1^2) \cos 2\alpha. $

B-4

Points on the circle will of course hold to $ x^2 + y^2 = r^2, $ so this simplifies, after using the earlier result for $ \cos 2\alpha, $ to $ x_1 x_2 + y_1 y_2 = r^2 - \frac{A^2}{2}. $

The very same strategy will give us $ x_2 x_3 + y_2 y_3 = r^2 - \frac{B^2}{2}. $

We can combine these equations by subtracting one from the other, giving us $ x_2(x_3 - x_1) + y_2(y_3 - y_1) = \frac{A^2 - B^2}{2}. $

At this point, we can start reinflating our center-relative coordinates. Within the first parentheses, we have $ r_x - c_x - p_x + c_x, $ and likewise within the second set. We soon get $ (q_x - c_x)(r_x - p_x) + (q_y - c_y)(r_y - p_y) = \frac{A^2 - B^2}{2}. $

Now, everything but $c_x$ and $c_y$ here are constants. We can reduce the clutter a bit by grouping them, say as $ D = -(r_x - p_x), E = -(r_y - p_y), $ and $ F = q_x D + q_y E + \frac{A^2 - B^2}{2}. $ This will give us $ Dc_x + Ec_y = F, $ the equation of a line of potential centers.

At this point, we are still at the impasse we were in before. We need to impose more constraints on the line.

We still have the relationship between $ \mathbf{r} $ and $ \mathbf{p} $ to exploit. As before, we will come up with $ x_1 x_3 + y_1 y_3 = r^2 - \frac{C^2}{2}. $ We can combine this as before with either of the other equations to bring in $ \mathbf{q} $, for instance as $ x_1(x_3 - x_2) + y_1(y_3 - y_2) = \frac{A^2 - C^2}{2}. $ This will give us another line as $ Gc_x + Hc_y = I. $

We can arrange this to put $c_y$ totally in terms of $c_x,$ for instance $ c_y = \frac{F - Dc_x}{E}. $ We can then feed it into the second equation, for $ Gc_x + \frac{H(F - Dc_x)}{E} = I, $ or $ \left(G - \frac{HD}{E} \right)c_x = I - \frac{HF}{E}. $ Multiplying by $E$ and rearranging, this is $ c_x = \frac{EI - HF}{EG - HD}. $

(TODO: EG - HD = 0)

Now that we have $c_x,$ we can feed it back in to get the equation for $c_y.$ In the event that $E$ is 0, we can use the second line equation to get it.

Now that we have actual values for the center, we can lock down our earlier center-relative points, say $x_1$ and $x_2.$ Thus, we can choose one of them arbitrarily and solve $ r = \sqrt{(p_x - c_x)^2 + (p_y - c_y)^2}. $ (No need to take negative roots.)

This process might sound a bit daunting, but it boils down to some fairly tight code:

local sqrt = math.sqrt

function Circumcircle ( px, py, qx, qy, rx, ry )
  -- Squared side lengths.
  local A2 = (qx - px)^2 + (qy - py)^2
  local B2 = (rx - qx)^2 + (ry - qy)^2
  local C2 = (px - rx)^2 + (py - ry)^2

  -- Center lines.
  local D, E = px - rx, py - ry
  local F = qx * D + qy * E + (A2 - B2) / 2
  local G, H = qx - rx, qy - ry
  local I = px * G + py * H + (A2 - C2) / 2

  -- Solve for the circumcenter.
  local cx, cy = (E * I - H * F) / (E * G - H * D)

  if E^2 < 1e-12 then -- choose from non-vertical line of centers
    cy = (I - G * cx) / H
  else
    cy = (F - D * cx) / E
  end

  -- Solve for the circumradius.
  return cx, cy, sqrt( (px - cx)^2 + (py - cy)^2 )
end

Frequently it will be the case that a lot of work leads to a nice formula. With some of the ideas in the next article we can make this even more concise.

EXERCISES

1. Find trilinear coordinates for the circumcenter.

2. Find the circumcircles of both a triangle and its orthic triangle. What can we say about the radii of these two circles?