Today’s guest tutorial comes to you courtesy of X.
Personal space invasion (M)
Recall the definition of the circle: all points a given distance from a common center. Now imagine the situation where we have two circles, not necessarily with the same radius. What would have to be true for them to just touch?
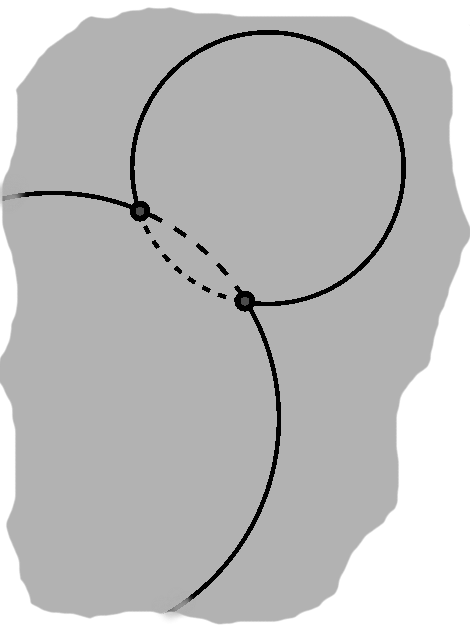
When circles do touch, this means that a point on one circle also belongs to the second circle. We are probably not talking about the trivial case where two circles of equal radius overlap, in which cases this is so for all points. Typically, what we do mean is that the circles interpenetrate—there are two intersections then, in fact, the first when one circle crosses the other going in, the second on the way out. This is true from the point of view of either circle.
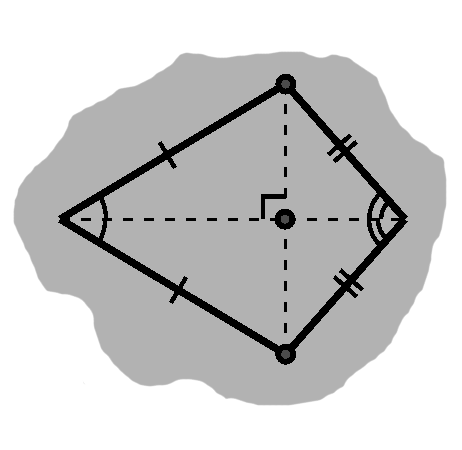
The arcs themselves are interesting, but we can do some other things too. For one, we can draw a line segment between the two intersection points. Furthermore, we can draw line segments from each point to the circle centers, giving us two triangles. Now, those intersection points are, of course, on the circles, so the distance to each respective circle is the radius. In other words, in each triangle, the two lines emerging from the center are equal: this is an isosceles triangle. The angle between them is obviously equal to itself. By side-angle-side, such a triangle is equal to itself. This seems a little silly, but it tells us that we could take the mirror image of the triangle. It follows from this that the other two angles are equal.
Now, consider what happens when we split this triangle down the middle. We then have side-angle-side again! One side is the radius, we just saw that these angles are equal, and the other side is half of the original length. The angle formed by the dividing line must therefore be the same, which makes these right triangles.
The same thing will happen on both sides. The line between the points of intersection is called a radical line, and as we see it happens to be perpendicular to the line between the circles' centers.
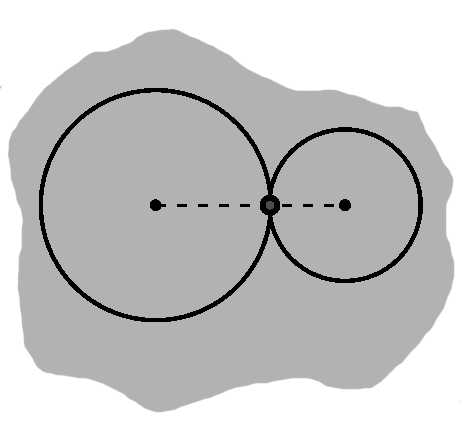
As the circles draw apart, these "in and out" arcs shrink. In other words, their arc lengths diminish, though obviously the circles (to which the arcs belong) are not changing size. Rather, the arc angles are narrowing. When they hit zero, the arcs "enter" and "leave" at the same point. Naturally, the triangles collapse as well, and thus so does the radical line, in fact to this point.
Indeed, this happens to be the point where the circles "just touch". The distance between the centers when this occurs is exactly the sum of the circles' radii: $ \sqrt{(center_{1,x} - center_{2,x})^2 + (center_{1,y} - center_{2,y})^2} = r_1 + r_2. $ (If we will not directly use this distance, but need only compare against it, we may square both sides.)
Now, when the circles were mashed up against one another, this distance was somewhat less. Going the other way, we know when they exceed this distance, the circles are separated and do not touch.
It is worth considering the first case a little more. In particular, when one circle is smaller than the other, it might actually be completely inside the other, without touching its boundary.
As we saw, we know that it is one or the other when the distance between centers is less than the sum of the radii. That distance is key. We already know how far the smaller circle is from the center, so in a sense we have "used up" that much radius, and there is some amount left. If the smaller circle's radius is not enough to make up the difference, it is completely contained. Otherwise, it touches the boundary.
(NOTES: Intersecting chord midpoints)
Tangent lines (N)
To get back to points on the circle, for any angle we can of course just find the cosine and sine.
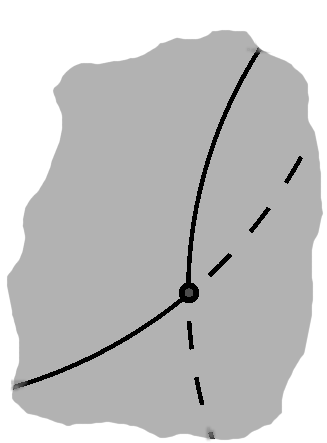
By construction, this is the difference between that point and the center. If we follow the same direction one unit out, we would also have a direction pointing away from the circle, a so-called surface normal.
Now, locally, this direction would be pointing straight up from the circle. If we went straight to the left or right in either direction, we would miss any more of the edge: since points are a radius away, and they have to spend some of that in the curve itself, the space will be empty there.
To go straight left and right implies going 90° away from straight up.
Since the normal's equation is that of the position, we can find one of these candidates by taking the respective measurements: $ x = \cos(\theta + 90^{\circ}) $ and $ y = \sin(\theta + 90^{\circ}). $ We find that $ \cos(\theta + 90^{\circ}) = -\sin\theta $ and $\sin(\theta + 90^{\circ}) = \cos\theta. $
These are useful identities in their own right (as are the variants where we subtract 90°, which will have signs flipped).
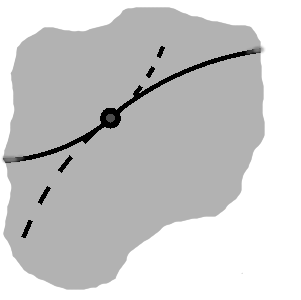
These components describe a tangent line, which only touches the circle at this point. (Although the reasons behind the name are the same and they sometimes arise in the same situation, this is different from the trigonometric function described above.)
Together with the normal, these two describe a sort of local coordinate frame above the circle. The next article will explore this idea in more depth.
(NOTES: Can use to "swim" along the surface when combined with re-projection, as in boids)
One example of how to apply this is to string circular arcs together nicely. Given two arcs, we can of course just line up one point from each. This can be a bit jarring, though.
If the tangents are pointing in the same (or opposite) directions, however, we have a perfect fit. This is the distinction between C0 and C1 continuity.
Certain functions lend themselves to nice approximations via circular blending curves, so this is a useful part of our toolkit.
In fact, curves assume this behavior locally. In addition to the tangent, the notion of curvature asks what the circle looks like locally, namely its radius.
We can also interpret a segment under this idea. One endpoint is taken as the center, while the offset of the second is converted to polar form. We then take its tangent. This will apply with any length.
A line is its own tangent. Naturally we might suspect it has no curvature. This would comport with it being an infinitely wide circle.