Today’s guest tutorial comes to you courtesy of X.
Some angle relationships
When placed side by side, two right angles will form a straight line. More generally, any two angles that do so are said to be supplementary. A pair that combine to form a right angle, on the other hand, are complementary.
Since an angle may be adjacent to an angle on each side, it might in fact be supplementary to both of them.
Furthermore, we can say the same about the supplementary angles themselves. We already know about the original angle, of course, but each one might supplement another angle, equally wide.
In fact, we would then have the situation of figure B-4, with the fourth and final angle being shared as well. In the end, we have a couple pairs of equal angles. These so-called vertical angles arise whenever two lines cross.
(NOTES: Loosen up a bit: describe and show a supplementary angle... then mention that we had to extend one of the sides to get the line we were completing... since an angle corresponds to two sides, we have another line, so supplementary to that as well... but the measure will be the same... we still have a fourth angle, but notice it's also flush with these lines, so has the original measure... then describe vertical, and tie it to crossing lines)
Drawing parallels
(NOTES: If we go the overlap route, which is likely, it seems much better to approach this using I-1 and I-2, along with the material for the same... we can still use some of what follows here... this might also let us cut some of the awkward "rectangles have parallel sides" bit in the next section)
(NOTES: The main thrust is that, because two sides already coincide as the transversal, the alternate angles situation means that the other two sides must be oriented the same way... "we call this parallel", etc.)
We have only been considering segments of lines, rather than the real deal. A segment begins in one location and ends in another, whereas lines continue in either direction indefinitely.
Lines are unbounded, but still pass through points. Selecting any two of them will give us the endpoints of a segment within the line. Conversely, the presence of a segment suggests the broader line embedding it.
Each of a triangle's three sides is a segment that can be understood as part of a line. This is rather precarious, of course: nearly any change in position will shift the side outside the line.
Parallel movements, however, will keep this relationship intact. These follow the direction of the line in question; the side will simply slide backward or forward along the line. If we move the entire triangle at once, we get something like figure G-1.
We can draw some useful inferences by considering the triangle before and after this movement as distinct.
Because the triangle only underwent a straight-line motion, without being flipped or rotated, its sides retain their same directions as well: the segments are parallel. For instance, this describes the two sides with double slash marks in figure G-1.
Naturally, since the sides never change direction, the angles between them are preserved as well. In fact, beyond motivating this insight, an underlying triangle is not even necessary. Whenever we have parallel segments sliced by a third one, we end up with several corresponding angles. The arcs in figure G-1 represent one of these equal pairs.
Two of the triangle's corners belong to the side embedded in the line, with the remaining one outside. When we move the triangle, however, this point traces a second line, as shown in dashes in figure G-1. Since the two share the same direction, these lines are also parallel.
Because parallel lines or segments follow the same direction, the distance between them will never change. In figure G-1, for instance, the triangles' heights—with the segments inside the line as bases, of course—will report the same distance separating the two lines. Parallel objects either never meet or completely coincide already.
EXERCISES
1. Demonstrate the midpoint theorem: if we connect the midpoint of one side with the midpoint of another, the segment between them will be half as long and parallel to the remaining side.
It All Adds Up
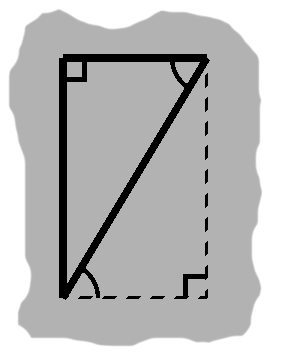
We can also go the other way. Given a right triangle, we make a copy of it. A couple rigid motions will then bring the two together, forming a rectangle as in figure I-1.
Notice the arcs, indicating a pair of alternate angles. When one line crosses two others, we will have a Z-like configuration, with this sort of arrangement of angles around the central segment. In this example we began with congruent triangles, so the angles are equal as well.
Once again, this particular example introduces the idea, but any sort of triangle will do. In fact, the only real necessity is that we have three segments forming a Z, with two of them being parallel.
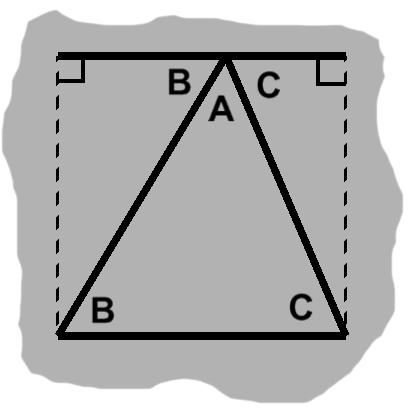
We can see why this is so in figure I-2. Even if we have a rather generic triangle, knowing its altitude will let us carve out a right triangle, at which point we can build a rectangle as before.
More importantly, some of our earlier concepts come together. Since we have parallel sides, we get corresponding angles as well, say $A$ and $B$. We also have a third angle that is both vertical to $A$ and alternate to $B$. We see this sort of relationship in figure I-2. We already know that corresponding and vertical angles are equal. The same must be true of alternate angles when we have parallel segments.
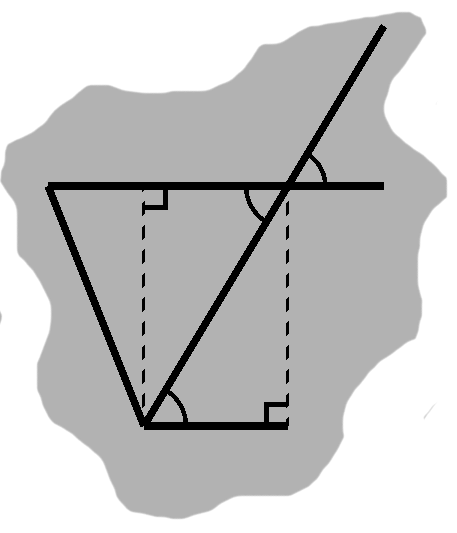
If we began with a fairly typical triangle, such as the one in figure H-4, we would need to add two right triangles to work our way back to a rectangle.
Doing so will tease out a pair of alternate angles from the triangle. Furthermore, these form a line with the remaining angle, as in figure I-3. Since their measures are the same as these three, the sum of the triangle's interior angles must be 180°.
This approach might seem to rule out triangles with either a right or an obtuse angle. Actually, if we turn such a triangle so that its longest side is on the bottom, we will have the previous scenario. Since the sum of angles is a feature of the whole triangle rather than a given side, we could stop here. The other possibilities are not too onerous, however, so we ought to go over them as well.
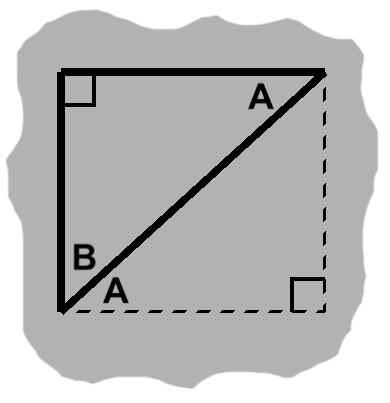
Right triangles are rather simple. Again, these are simply half rectangles, with parallel sides leading to equal alternate angles. Because it fills a corner, one of these angles will also complement the angle already found there. From figure I-4, for instance, we see that $ A + B = 90^{\circ}. $ As expected, $A,$ $B,$ and the right angle add up to 180°.
An obtuse angle, say $O,$ decomposes into a right angle and smaller adjacent angle. On their own, we already know how to attack the two triangles this gives us; a hybrid approach will get us the rest of the way.
We will have a situation like figure I-5. At the outset, we know that $ D + S = 90^{\circ} $ and $ C = O - 90^{\circ}. $ Because $S$ and $A$ form a line, the first of these can be rewritten as $ D + (180^{\circ} - A) = 90^{\circ}, $ or $ A = D + 90^{\circ}. $
Now, $ A + B + C = 180^{\circ}. $ Plugging in our recent findings, the left-hand side becomes $ (D + 90^{\circ}) + B + (O - 90^{\circ}). $ This simplifies to $ B + D + O = 180^{\circ}. $ All is well.
EXERCISES
1. What happens with four sides? Do we need to account for special cases?
2. What about the general case of $n$ sides ($n >= 3$)?