Today’s guest tutorial comes to you courtesy of X.
Angle addition
Continuing on the angle theme, recall how adjacent angles summed together.
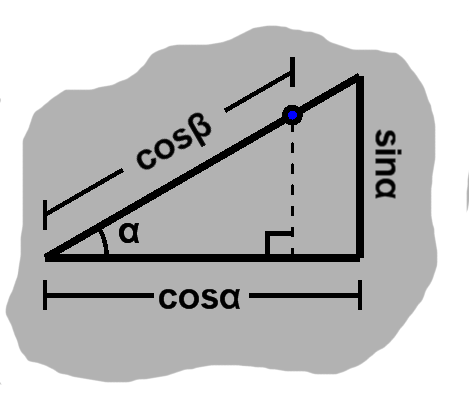
We begin with the triangle for one of these, as normal.
One for a second rests on top of the original triangle. This is where our opposite-adjacent abstraction comes to the fore, as it no longer aligns with the x-axis.
The right angle's corner on the second triangle rests on the hypotenuse of the first triangle, which has length 1 on the unit circle. The distance to this point is $ \cos\beta, $ the length of that side.
We can create a similar triangle from the first triangle, using this length as the common scale factor. Then by scaling the sides of the first triangle, the position of this corner is $ \vcomps{\cos\beta\cos\alpha}{\cos\beta\sin\alpha}. $
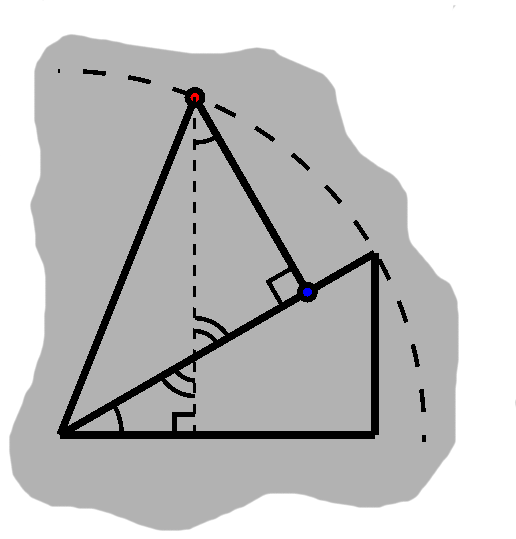
Of course, as with our two triangles, we can tease out the triangle for the combined angle, $ \alpha + \beta, $ which will have corner $ \vcomps{\cos(\alpha + \beta)} {\sin(\alpha + \beta)}. $
In doing so, we flush out several smaller triangles. On the bottom, we have one similar to the first triangle. As we saw in the previous article, vertical angles are equal, so that carries over to the triangle above. Furthermore, angles sum to 180°, so the angle up top is $\alpha.$
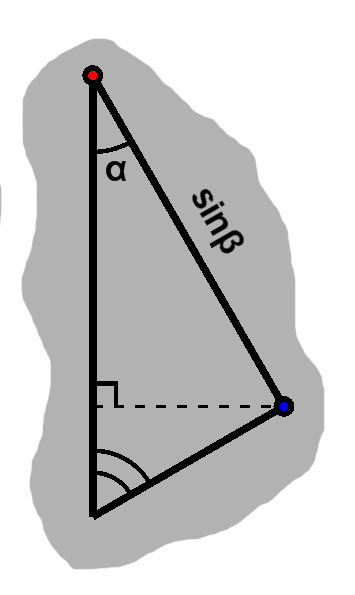
We can further split the above triangle into two smaller right triangles by cutting it horizontally. Up top, we again fill in the missing angle from the sum to 180° (As an aside, note that these both happen to be similar to the first triangle.)
This new top triangle has hypotenuse $ \sin\beta. $ Thus, it has horizontal length of $ \sin\alpha\sin\beta $ and vertical length $ \cos\alpha\sin\beta. $
The corner coincides with that of the second triangle, whereas the upper one is the position of the new angle. Finally: \begin{align} \cos(\alpha + \beta) & = \cos\beta\cos\alpha - \sin\alpha\sin\beta \\ \sin(\alpha + \beta) & = \cos\beta\sin\alpha + \cos\alpha\sin\beta \end{align}
The tangent follows readily enough: \begin{align} \tan(\alpha + \beta) = \frac{\cos\beta\sin\alpha + \cos\alpha\sin\beta}{\cos\beta\cos\alpha - \sin\alpha\sin\beta} \end{align} Nothing really stands out about this formula. We can employ the technique from our previous article, however, of "multiplying by 1". In particular, $1 = \frac{\cos\alpha\cos\beta}{\cos\alpha\cos\beta}.$
This spreads like wildfire among the terms! The cosines disappear; the sines become tangents: \begin{align} \tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta} \end{align}
Other quadrants
This analysis only applies to the first quadrant.
For the rest, we consider that adjacent angles sum together. Since (a + b) + c = a + (b + c) and so on, we can express a sum of angles wider than 90 degrees as 90 + c.
In that case, we can look at it as rotated by 90 degrees. Our results agree with the formula!
We can do this again with 180 and 270 degrees. Seemingly we wrap around after 360.
Notice some symmetry!
Double angles
We can derive some useful results immediately.
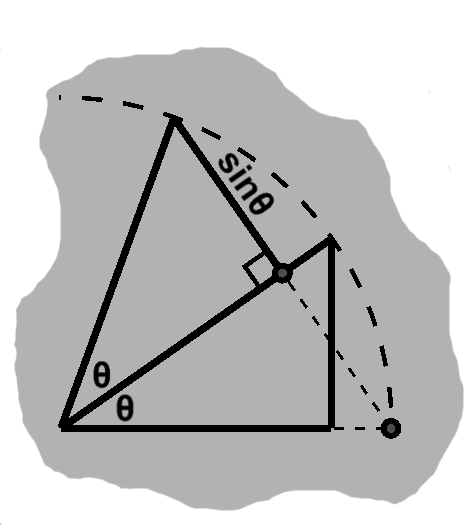
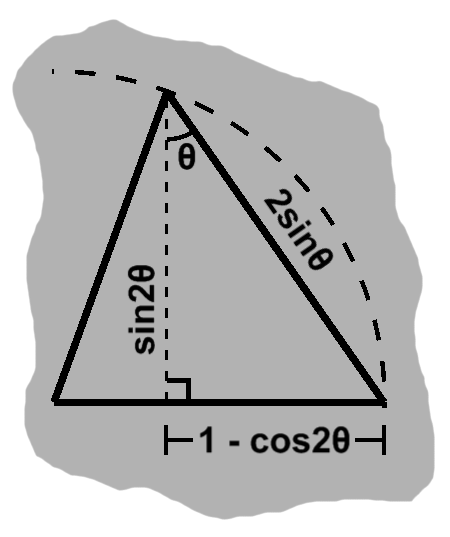
\begin{align} \sin(\theta + \theta) & = \cos\theta\sin\theta + \cos\theta\sin\theta \\ \sin 2\theta & = 2\cos\theta\sin\theta \end{align}The two corners of this side are on the unit circle, so this is a chord. Usually we will simply have a central angle, rather than double angle than found here, so in the general case: \begin{align} \textrm{crd}\,\theta = 2\sin\frac{\theta}{2} \end{align}
The altitude is its adjacent side, of course, and the hypotenuse $ 2\sin\theta. $ This confirms our identity; in fact, it would have been another way to derive it.
\begin{align} \cos(\theta + \theta) & = \cos\theta\cos\theta - \sin\theta\sin\theta \\ \cos 2\theta & = \cos^2\theta - \sin^2\theta \end{align} This is reminiscent of our very first identity. Indeed, we can exploit this to flush out some new ones: \begin{align} \cos 2\theta + 1 & = \cos^2\theta + (1 - \sin^2\theta) \\ & = 2\cos^2\theta \\ \cos 2\theta & = 2\cos^2\theta - 1 \end{align} as well as \begin{align} \cos 2\theta & = (1 - \sin^2\theta) - \sin^2\theta \\ & = 1 - 2\sin^2\theta \end{align} These in turn lead to the so-called power reduction formulae: \begin{align} \cos^2 \theta & = \frac{1 + \cos 2\theta}{2} \\ \sin^2 \theta & = \frac{1 - \cos 2\theta}{2} \\ \tan^2 \theta & = \frac{1 - \cos 2\theta}{1 + \cos 2\theta} \end{align} From the earlier angle addition: \begin{align} \tan 2\theta & = \tan(\theta + \theta) \\ & = \frac{2\tan\theta}{1 - \tan^2\theta} \end{align} From this we can eke out one last identity for the cosine: \begin{align} \frac{\sin 2\theta}{\tan 2\theta} & = 2\cos\theta\sin\theta\frac{1 - \tan^2\theta}{2\tan\theta} \\ \cos 2\theta & = \cos\theta\sin\theta(1 - \tan^2\theta)\frac{\cos\theta}{\sin\theta} \\ & = \frac{1 - \tan^2\theta}{\sec^2\theta} \\ & = \frac{1 - \tan^2\theta}{\tan^2\theta + 1} \end{align} We can then turn it back around and add another for sine: \begin{align} \tan 2\theta\cos 2\theta & = \frac{2\tan\theta}{1 - \tan^2\theta}\frac{1 - \tan^2\theta}{\tan^2\theta + 1} \\ \sin 2\theta & = \frac{2\tan\theta}{\tan^2\theta + 1} \end{align}EXERCISES
1. What form would a cosine-based chord formula take?
2. Derive $\tan 2\theta$ geometrically.
3. Find the triple angle formulae: $\cos 3\theta, \sin 3\theta, \tan 3\theta.$ Try generalizing to $n\theta.$
Half angles
We can go the other way, halving angles rather than doubling them.
Half angles will double into normal angles, so we can employ our previous results. For instance: \begin{align} \cos 2{\theta \overwithdelims ( ) 2} & = 1 - 2\sin^2\frac{\theta}{2} \\ 2\sin^2\frac{\theta}{2} & = 1 - \cos\theta \end{align} This is useful in its own right. The versine, $1 - \cos\theta,$ has known issues when used in floating point calculations, whereas this substitution is much more stable. Appropriate identities and the algorithms to drive them are key to robust numerical software.
Proceeding further: \begin{align} \sin\frac{\theta}{2} = \pm\sqrt{\frac{1 - \cos\theta}{2}} \end{align} The choice for $\pm$ will depend upon what quadrant contains the half angle.
Continuing: \begin{align} \cos^2\frac{\theta}{2} & = 1 - \sin^2\frac{\theta}{2} \\ & = 1 - \frac{1 - \cos\theta}{2} \\ \cos\frac{\theta}{2} & = \pm\sqrt{\frac{1 + \cos\theta}{2}} \end{align}
EXERCISES
1. Could these formulae be adjusted to supply the appropriate sign? If so, would these new versions be drop-in replacements, or would there be caveats?
2. Find some half angle formulae for the tangent involving normal angles and no square roots.